Halo sobat semua.! salam hangat dan sejahtera untuk kalian semua. Pada pembahasan kali ini, kembali akan edmodo uraikan pembahasan tentang materi makalah yang terhimpun dalam materi aljabar, yakni tentang determinan matriks, berikut ulasannya.

Pembahasan mengenai determinan metriks yang mana meteri ini di terhimpun dalam bidang al jabar linear, definisi dari determinan sendiri mengacu kepada sebuah hasil atau nilai yang diperoleh berdasarkan penghitungan atas unsur matriks persegi.
Seperti misalnya Determinan matriks A yang mana penulisannya menggunakan sebuah simbol, yakni : det(A), det A, atau |A|.
Kemudian Determinan juga kerap dianggap merupakan sebuah faktor atas penskalaan transformasi yang diterangkan dengan matriks.
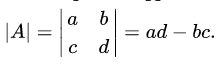
Kemudian jika bentuk dari pada matriksnya 3 × 3 matrix A, maka untuk mencarinya bisa dengan menggunakan sebuah rumus yakni sebagai berikut :

Kemudian penggunaan Rumus Leibniz biasanya bisa digunakan untuk menentukan determinan matriks n × n , berikut ini rumusnya:

Selain kita juga bisa menggunakan sebuah Metode eliminasi Gauss untuk menentukan nilainya.
Berikut ini sedikit contoh dari determinan matriks yang diterangkan seperti di bawah ini:

Kemudian penghitungan dapat dilakukan dengan menggunakan sebuah matriks seperti di bawah ini:

Keterangan:
Pada keterangan di sini, yang perolehan B didapatkan dari A dengan cara adanya apenambahan −1/2× pada baris pertama dan juga baris kedua, maka akana memperoleh det(A) = det(B).
Selanjutnya pada nilai C yang mana didapatkan dari B dengan cara menambahkan kolom pada bagian pertama dan juga kolom yang ketiga, Maka akan memperoleh det(C) = det(B).
Sedangkan pada D perolehannya berhasil di dapat dari C yakni dengan cara melakukan penukaran terhadap kolom kedua dengan yang ketiga, maka akan amemperoleh det(D) = −det(C).
Kemudian mengenai Determinan matriks yang berbentuk segitiga D adalah hasil dari sebuah bilangan perkalian diagonal yakni : (−2) · 2 · 4.5 = −18.
Maka oleh sebab itu berdasarkana penjabaran diatas bisa kita simpulkan hasil dari det(A) = −det(D) = +18.
Sifat-Sifat Determinan Matriks
Di bawah ini akan edmodo sajikan pula pembahasana terkait mengenai determinan metriks, yakni mengenai sifat yang dimiliki oleh determinan matriks
1. Apabila setiap unsur elemen yang terdapat pada salah satu baris/kolom memiliki nilaia penjumlahan yakni = /sama dengan nol, maka sudah bisa kita pastikan bahwa determinan matriks tersebut juga bernilai nol.
Sebagai Contoh :

2. Apabila dari setiap unsur elemen yang ada dari salah satu baris/kolom mempunyai nila yang sama dengan sejumlah elemen yang terdpaat pada baris/kolom lain, maka nilai dari determinan matriks tersebut juga nol.
Sebagai Contoh B =

(Hal ini disebabkan adanya kesamaan pada sejumlah elemen yang terdapat pada baris ke-1 dan 3.
3. Apabila sejumlah elemen yang terdapat dari salah satu baris/kolom adalah suatu nilai kelipatan dari sejumlah elemen pada baris/kolom lain, maka nilai dari pada determinan matriks tersebut nol.
Sebagai Contoh A =
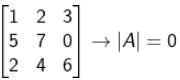
(Hal ini disebabkan adanya kesamaan dari sejulah elemen kelipatan pada baris ke-1).4. |AB| = |A| ×|B|5. |AT| = |A|, yang mana untuk AT ialah merupakan transpose atas matriks A.6. |A–1 = –1 1/A , sedangkan untuk A–1 merupakan bentuk invers dari matriks A.
Namun pembahasanaa Materi invers akan edmodo jelaskan juga pada pembahasan subbab selanjutnya ).7. |kA| = kn |A|, yang mana untuk A ordo n × n yang mana bentuk k disini merupakan suatu konstanta.
Baca Juga : Pertidaksamaan Linear Satu Variabel
Contoh Soal dan Pembahasannya

Setelah edmodo uraikan secara detail pembahasan mengenai dterminan metriks, mulai dari pengertian, rumus dan sifatnya, maka tibahlah kita dipengujung pembahasan, yang mana di bawah ini akan sedikit edmodo sajikan soal latihan, semoga dapat sobat semua jadikan sebagai bahan acuan untuk mengerjakan berbagai soal terkait tentang determinan metriks.:
Soal Pertama Determinan Ordo 2 x 2
Contoh 1:
Perhatikan pada soala latihan yang ada di bawah ini, kemudian tentukan dan hitungalah pada sejumlah nilai determinan pada sebuah matrik di bawah ini:
Keterangan Pembahasan:
M=
| 5243 |
Jawabannya :
det(M) =
| 5243 |
Maka hasil dari ulasan diatas sudah kita dapatkan = (5 × 3) – (2 × 4) = 7
Contoh 2:
Kemudian pada soal yang kedua tentukanlah dan hitung berapakah hasil dari nilai determinan pada sebuah matrik di bawah ini:
Keterangan Pembahasan:
Untuk N=
| -6-13-2 |
Jawabannya:
det(N) =
| -6-13-2 |
Maka hasil yang diperoleh dari tahapan pengerjaan diatas adalah = ((–6) × (-2)) – (3 × (–1)) = 15
Soal Kedua Determinan Matriks Ordo 3 × 3
Perhatikan uraian pertanyaan berikut ini :
Baca Juga : Persamaan Linear Dua Variabel
Apabila sudah kita ketahui bahwa pada sebuah matriks A, yang mana metriks tersebut adalah sebuah matriks yang berbentuk persegi dan memiiliki dua ordo /ordo dua. Maka tentukan dan hitunglah:
A=
| abcd |
Apabila ingin mengerjakan soal ini, maka kita bisa menggunakan sebuah rumus det A seperti di bawah ini:
det(A) =
| abcd |
Jadi hasil dari perhitungan dengan menggunakan rumus diatas adalah = ad – bc
Contoh 1:
Perhatikan soal latihan berikut : Tentukan dan Hitungalah berapakah hasil dari nilai determinan pada matrik di bawah ini:
M=
| 5643 |
Keterangan Pembahasan:
det(M) =
| 5643 |
Jadi sudaha diperoleh jalan sebagai berikut = (5 × 3) – (6 × 4) = 16
Contoh.2
Soal latihan selanjutnya, tentukanlah dan Hitungalah berapakah hasil determinan pada matrik di bawah ini:
N=
| -6-23-2 |
Keterangan Pembahasan:
det(N) =
| -6-23-2 |
Maka kita memperoleh jalan seperti = ((–6) × (-2)) – (3 × (–2)) = 18
Soal Ketiga Determinan Matriks Ordo 3 × 3
Perhatikanlah soal latihan berikut ini :
Yang mana ada yang dapat dilakukan untuk menghitung dan menentukan determinan pada sebuah metriks berordo 3×3 ini, yakni seperti berikut:
- Yang pertama adalah menggunakan Metode Sarrus
- Yang kedua menggunakan Metode Minor-Kofaktor
Adapun langkah yang sangat mudah yang bisa kita lakukan dan hampir kerap digunakan untuk menentukan suatu determinan metriks berordo 3×3 adalah metode Sarrus.
Metode Sarrus
Metode ini bisa kita gambarkan seperti, apabila kita memiliki matriks A berordo 3×3 seperti di bawah ini:
A =
| a11a12a13a21a22a23a31a32a33 |
Maka langkah yang dapat kita gunakan atau lakukan untuk menghitung dan mencari determinannya adalah dengan menggunakan skema gambar sebagai berikut:
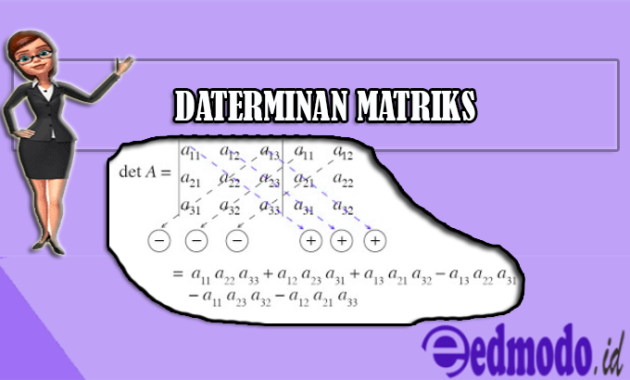
Untuk lebih jelasnya terkait rangkaian pengerjaan soal metriks ini, maka edmodo berikan contoh latihan di bawah ini :
Contoh 1:
Perhatikan soal latihan di bawah ini : Hitung dan tentukanlah berapakah Nilai Determinan pada sebuah matriks ordo 3×3 di bawah ini:
A =
| 23454371 |
Keterangan Pembahasan:
Jadi berdasarkan langkah diatas dapat kita simpulkan nilai determinan pada sebuah matriks di atas adalah:
det(A) =
| 23454371 |
| 23547 |
Perhatikan rangkaian pengerjaannya :
det(A) = 2.4.1 + 3.3.7 + 4.5. – 4.4.7 – 2.3. – 3.5.1
= 8 + 63 + – 112 – – 15
= – 56
Contoh 2:
Soal latihan selanjutnya adalah : Hitunglah berapakah hasil dari nilai Determinan pada sebuah matriks ordo 3×3 di bawah ini:
B =
| 123214312 |
Keterangan Pembahasan:
Jadi sudah kita peroleh bahwa nilai determinan pada sebuah matriks di atas adalah seperti di bawah ini:
det(B) =
| 123214312 |
| 122131 |
det(A) = (1.1.2) + (2.4.3) + (3.2.1) – (3.1.3) – (1.4.1) – (2.2.2)
= 2 + 24 + 6 – 9 – 4 – 8
= 11
Bagaimana sob, tentunya mudah bukan?!! Semoga Tuhan Yang Maha Kuasa memberikan pemahaman kepada hambanya yang mau berusaha dan belajar.
Sekian dulu ya sob.! Mohon maaf apabila dalam penyampaian terdapat kata atau kalimat yang kurang falid atau kurang berkenan dihati sobat edmodo.id semua. Kepada kalian edmodo.id ucapkan mohon maaf dan Kepada Allah Swt edmodo.id mohon ampun yang seluas – luasnya.
