Persamaan Matriks – ialah merupakan suatu kumpulan pada bilangan yang telah disusun dengan berdasarkan baris dan juga pada kolomnya, pada bilangan yang ada matriks tersebut dengan cara elemen matriks.
Pada elemen matriks ini dapat disusun secara vertikal (kolom) maupun dengan cara horizontal (baris).
Biasanya pada persoalan matematika ini menggunakan dengan matriks ialah untuk mencari nilai pada persamaan linear, fungsi linear, maupun transformasi linear.
Contohnya untuk sebuah matriks yang mempunyai sebagian baris dan n yaitu sebagai kolom maka dapat dituliskan m x n atau dapat disebut dengan matriks atau dengan ordo m x n.
Bentuk ax = b dan xa = b contohnya a, b, dan juga x ialah merupakan matriks – matriks yang berordo 2 × 2, dengan matriks a dan b sudah diketahui elemennya tersebut.
Sedangkan dengan matriks x belum diketahui elemen – elemennya dan Matriks x ini bisa ditentukan apabila a memiliki invers atau disebut dengan matriks nonsingular.
Definisi Matriks

Dengan cara yang sederhana ini matriks dapat diartikan sebagai suatu kumpulan pada bilangan yang telah disusun didalam baris maupun kolom.
Pada bilangan – bilangan yang telah disusun pada matriks ini sering disebut dengan elemen – elemen matriks.
Dengan ukuran matriks ini dengan cara ordo matriks contohnya matriks berordo 3 x 2, jadi matriks ini berukuran 3 baris dan juga 2 kolom.
Dengan berdasarkan ordo pada matriks ini dapat di susunan dengan elemen – elemennya, dan ada beberapa jenis matriks diantaranya yaitu matriks kolom, matrisk baris, dan matriks persegi, pada matriks persegi panjang, matriks diagonal, matriks segitiga, dan ada jenis yang matriks yang lainnya.
Kedua matriks ini bisa dijumlahkan maupun dikurangkan apabila ordo kedua matriksnya sama, dan pada penjumlahan maupun pada pengurangan matriks yang telah dilakukan dengan menjumlahkan maupun mengurangkan masing – masing elemen yang sesuai dengan kedua matriks tersebut.
Baca Juga : Rumus Abc
Materi Persamaan Matriks

ax = b↔ a–1(ax) = a–1b↔ (a–1a)x = a–1b↔ ix = a–1b↔ x = a–1b
Dari persamaan yang terakhir ini nampaknya bahwa kedua ruas yang dikalikan dari kiri oleh a–1 sampai diperoleh bentuk penyelesaiannya x = a–1b.
Supaya dapat menyelesaikan persamaan matriks yang berbentuk xa = b bisa ditentukan dengan cara mengalikan kedua ruasnya dari kanan dengan a=–1 sampai dapat diperoleh penyelesaiannya x = ba–1 sebagai berikut yaitu.
xa= b↔ (xa) a–1 = ba–1↔ x(aa–1) = ba–1↔ xi = ba–1↔ x = ba–1
Maka dari itu, kita dapat memperoleh penyelesaiannya x= ba–1.
Dengan ini, bisa kita simpulkan sebagai berikut ini yaitu, pada penyelesaian persamaan matriks ax = b ialah x = a–1b.
Pada penyelesaian persamaan matriks xa = b ialah x = ba–1.
supaya kita dapat lebih jelas lagi, marilah perhatikan contohnya sebagai berikut ini.
Diketahui A =
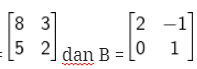
Tentukan nilai matriks x yang memenuhi
A. ax = b ; b. xa = b.
Jawabannya :
Karena det a = 16 – 15 = 1 ↔ 0 maka matriks a memiliki invers, apabila dicari inversnya, maka kalian akan memperoleh a–1 =
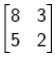
Cobalah kalian tunjukkan.
Maka dari itu, kita dapat tentukan sebagai berikut ini.
Contoh Soal Persamaan Metriks

P dan Q ialah matriks 2×2 seperti yang kita lihat di bawah ini :
P =-2 5-1 3Q =-5 4-1 1
Apaila P-1 ialah invers dari juga matriks P dan Q-1 ialah merupakan invers dari matriks Q, maka dari determinan matriks P-1.q-1 ialah ?
- A. 223
- B. 1
- C. -1
- D. -10
- E. -223
Pembahasannya :
Supaya kita mengetahui suatu determinan dari P-1.q-1 ada baiknya kita mencari invers terlebih dahulu dari masing – masing matriks tersebut.
Apabila diberikan suatu matriks dengan ordo 2×2 sebagai berikut yaitu :
a = -a b-c d
Maka dari invers matriks ini bisa kita rumuskan sebagai berikut yaitu :
a-1 = 1 .-d -b-ad – bc-c a
Dengan berdasarkan rumus tersebut maka kita memperoleh :
Invers dari matriks P
- ⇒ P =-2 5-1 3
- ⇒ P-1 = 1 .-3 -5-2 (3) – 1(5)-1 2⇒ P-1 =-3 -5–1 2
Invers dari matriks Q
- ⇒ Q =-5 4-1 1
- ⇒ Q-1 = 1 .-1 -4-5 (1) – 1(4) -1 5⇒ Q-1 =-1 -4 – -1 5
Selanjutnya marilah kita ambil dari hasil perkalian dari invers matriks tadi yaitu, apabila di berikan dua matriks berordo 2×2 sebagai berikut ini :
a = -a b- dan b = -m n – c do p
Maka dari perkalian yang bisa selesai dengan berdasarkan aturan perkalian matris, yaitu :
a.b = -am + bo an + bp-cm + do cn + dp
Dengan berdasarkan konsep ini, maka kita perlu memperoleh :
- ⇒ P-1 = -3 – 5- dan Q-1 = -1 -4 – -1 2-1 5
- ⇒ P-1.q-1 = -3 (1) + (-5) (-1) 3(-4) + (-5) (5) – (-1) (1) + 2 (-1) (-1) (-4) + 2(5)⇒ P-1.q-1 = -8 -37 – -3 14
Dari determinannya ialah :
- ⇒ |P-1.q-1| = 8(14) – (-37)(-3)
- ⇒ |P-1.q-1| = 112 – 111
- ⇒ |P-1.q-1| = 1
Jawabannya : B
- Diketahui dari persamaan matriks yaitu :
-a 4- + -2 b- =-1 -3-.-0 1- -1 cd -33 41 0
Nilai a + b + c + d =
A. -7d. 3b. -5e. 7c. -1
Pembahasannya :
Sesuai dengan konsep dari penjumlahan dan perkalian matriks, maka kita dapat memperoleh :
⇒ -a 4- + -2 b- = -1 -3-.-0 1–1 cd -33 41 0⇒ -a + 2 4 + b- =-1(0) + (-3) (1) 1(1) + (-3) (0)–1 + d c – 33(0) + 4(1) 3(1) + 4(0)⇒ -a + 2 4 + b- = -3 1- -1 + d c – 34 3
Berdasarkan dengan konsep pada kesamaan matriks, maka :
Nilai A ⇒ a + 2 = -3
⇒ a = -5
Nilai B yaitu :
⇒ 4 + b = 1
⇒ b = -3
Nilai C :
⇒ c – 3 = 3
⇒ c = 6
Nilai D :
⇒ -1 + d = 4
⇒ d = 5
Dengan hal ini kita dapat memperoleh :
⇒ a + b + c + d = -5 + (-3) + 6 + 5
⇒ a + b + c + d = 3
Jawabannya : D
- Jika diberikan matriks a, b, dan c sebagai berikut yaitu : A. =-2 -1- , B = -x+y 2- dan C = -7 2-1 43 y3 1
Apabila b – a = ct dan ct ini merupakan transpose dari matriks c, maka nilai x.y sama dengan ! A. 10 B. 15 C. 20 D. 25 E. 30
Pembahasannya :
Apabila diberikan suatu matriks ordo nya 2×2 sebagai berikut yaitu :
A = -a b-c d
Maka dari transpose matriks tersebut ialah :
At = -a c-b d
Berdasarkan konsep tersebut, maka transpose dari C adalah :
Ct = -7 3-2 1
Dengan ini kita dapat memperoleh :
⇒ B – A = Ct
⇒ -x+y 2- − -2 -1- =-7 3-3 y1 42 1⇒ -x+y − 2 2 − (-1)- =-7 3-3 − 1 y − 42 1⇒ -x + y – 2 3- =-7 3-2 y – 42 1
Dengan berdasarkan dari konsep kesamaan matriks, maka akan berlaku :
⇒Y – 4 = 1
⇒ Y = 5
Selanjutnya yaitu :
⇒X + y – 2 = 7
⇒ X + 5 – 2 = 7
⇒ X = 4
Maka dengna hal ini kita dapat memperoleh :
⇒ x . y = 4(5)
⇒ x . y = 20
Jawabannya : C
- Diketahui matriks a, b, dan c sebagai berikut yaitu : A = -3 0-, B = -x -1- dan, C = -0 -1-2 5y 1-15 5
Apabila At ialah merupakan dari transpose matriks a dan at. b = c, maka nilai dari 2x + y = A. -4 B. -1 C. 1 D. 5 E. 7
Pembahasannya :
Apabila diberikan suatu matriks ordo yaitu 2×2 sebagai berikut :
A = -a b-c d
Maka dari transpose matriks ini ialah :
At = -a c-b d
Dengan berdasarkan konsep ini, maka transpose dari a ialah :
At = -3 2-0 5
Maka dengan ini kita memperoleh :
⇒ At . B = C
⇒ -3 2- . -x -1- =-0 -1-0 5y 1-15 5⇒ -3(x) + 2(y) 3(-1) + 2(1)- = -0 -1-0 (x) + 5(y) 0(-2) + 5(1)-15 5⇒ -3x + 2y -1- =-0 -1-5y 5-15 5
Dengan berdasarkan konsep kesamaan matriks ini, maka berlaku :
⇒ 5y = -15
⇒ y = -3
Lanjutannya :
⇒ 3x + 2y = 0
⇒ 3x + 2(-3) = 0
⇒ 3x = 6
⇒ x = 2
Maka dengan demikian :
⇒ 2x + y = 2(2) + (-3)
⇒ 2x + y = 1
Jawabannya : C
5. Maka perlu diketahui ada sebuah persamaan matriks yang tidak lengkap yaitu sebagai berikut.
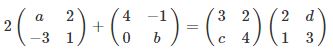
Maka carilah hasil dari 2a + b – 2c + d =
Pembahasannya :
Ada beberapa langkah untuk mengerjakan soal di atas, soal ini mirip dengan soal yang sebelumnya, anda dapat mengalikannya dengan angka 2 dan dengan matriks yang pertama sampai dapat.

Anda dapat membuat persamaan dengan setara antara ruas kanan dengan ruas kiri maka seperti iilah penyelesaiannya.
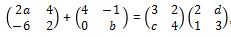
Maka kita perlu melakukan perkalian pada ruas yang kiri, sampai mendapatkan bentuk yang sama diantara matriks bagian ruas yang kanan dan juga pada bagian ruas kiri sebagai berikut ini.
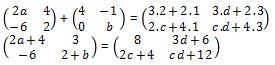
Apabila pada ruas kanan dan juga ruas kiri telah setara sampai anda dapat mencari nilai a, b, c, dan juga d.
- 2a+4 = 8, maka nilai a = 2
- 2 + b = cd + 12, maka nilai b = 15
- -6 = 2c + 4, maka nilai c = -5
- 3 = 3d + 6, maka nilai d = -1
Namun dari nilai 2a + b – 2c + d = 2.2 + 15 – 2(-5) + (-1) = 28
6. Diketahuilah matriks
Apabila C.O = A, Tentukanlah nilai det A
Pembahasannya :
Dalam mengerjakan soal tersebut, anda harus memahami konsep dari determinan matriks, dan dari sifat determinan matriks ini menyatakan bahwa apabila CO = A, maka det (C) x det (O) = det (A),
Dalam hal ini sampai anda menentukan det (A), namun anda cukup mencari nilai dari det (C) dan juga det (O).
det(C) = 2(6) – 4(5) = -8, det (O) = -1(2) – 1(0) = -2, sampai det (A) = -8 x -2 = 16.
Maka, nilai determinan pada matriks a ialah 16.
Penyelesaiannya :
Diketahui bahwa pada kedua matriks diatas saling invers, maka berlakunya syarat aa-1 = a-1a = I.
Jadi :

Sampai pada elemen baris yang pertama dan juga pada kolom yang pertama ini mempunyai persamaan yaitu sebagai berikut :
- 9(x -1) – 7x = 1
- 9x – 9 – 7x = 1
- 2x = 10
- x = 5
Maka, nilai x nya yaitu = 5
Sekian yang dapat disampaikan, semoga ulasan diatas bisa bermanfaat.
Baca Juga : Persamaan Kuadrat Baru
