Persamaan Kuadrat Baru – Contoh Soal dan Cara Mencarinya

by

Persamaan Kuadrat Baru – Definisi dari persamaan kuadrat sendiri ialah merupakan salah satu dari persamaan yang dimilki oleh variabel dengan pangkat yang tertinggi yakni adalah dua.

Kemudian bentuk dari grafik persamaan kuadrat yang berupa kurva yang melengkung dan mempunyai satu titik di puncak.

Yang mana pada titik puncak tersebut maksimumnya terdapat pada kurva yang telah terbuka ke bawah, sedangkan pada titik di puncak mimimal ada pada kurva yang telah terbuka ke atas.

Pembahasan pada persamaan kuaddrat ini merupakan sebuah cara yang kerap digunakan untuk menentukan persamaan kuaddrat yang baru.

Apabila sahabat sudah mengetahui rumus dari persamaan kuaddrat tersebut, maka dengan demikian sahabat juga bisa lebih mudah untuk menentukan persamaan dari kuadrat baru dan beserta akar – akarnya yang berbeda.

Dengan melewati halaman ini sahabat akan dapat mempelajari cara untuk menentukan persamaan kuadrat baru dan juga dari perrsamaan kuadrat awal yang telah diketahui.

Rumus Menentukan Persamaan Kuadrat Baru

Persamaan Kuadrat Baru
Persamaan Kuadrat Baru

Apabila kita sudah mengetahui rumusnya, maka nantinya rumus abc ini akan kita gunakan untuk menentukan akar perssamaan kuadratnya.

Lantas bagaimana caranya? nah dalam hal ini kita bisa menggunakan rumus yang umumnya sering digunakan agar kita bisa mengetahui hasil dari perkalian akar persamaan kuadrat. berikut ini rumusnya.

Rumus abc

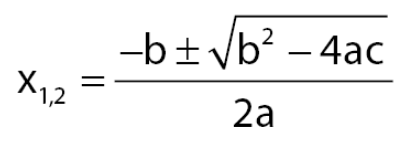
Rumus abc
Rumus abc

Di bawah ini sudah tersedia rumus untuk menentukan jumlah dan hasil perkalian akar persamaan kuadrat tersebut.

Rumusax² + bx + c = 0

Namun agar bisa menentukan persamaan, maka kita akan menggunakan akar kuadrat seperti berikut ini.

Persamaan kuadrat awalax² + bx + c = 0
Persamaan kuadrat barux² – ( x¹ + x²) x +x¹ . x² = 0

Jadi x¹ dan x²adalah sejumlah akar yang didapat dari persamaan kuadrat . Kemudian untuk mencari persamaan kuadratnya kita bisa menggunaka langkah sebagai berikut.

Langkah Menentukan Persamaan Kuadrat Baru

  • Harus menentukan jumlah dan juga perkalian pada akar – akar tersebut dengan persamaan kuadrat awal.
  • Harus menentukan jumlah dan juga perkalian pada akar – akar tersebut dengan persamaan kuadrat baru yang telah diketahui.
  • Harus membentuk persamaan kuadrat baru yang sesuai dengan rumus – rumus yang sudah di berikan di atas tadi : X2 – (X1 + X2) X + X1 ⋅ X2 = 0

Berikut ini edmodo.id akan memberikan contoh soal beserta cara menemukan dari persamaan kuadrat baru.

Kemudian akan diberikan juga contoh soal cara menentukan persamaan kuadrat baru dan juga pembahasannya marilah kita simak pembahasannya sebagai berikut.

Contoh Soal Persamaan Kuadrat

Pada pembahasan yang telah kami bahas diatas tadi telah memberikan rumus – rumus yang bisa di gunakan untuk menentukanpada persamaan kuadrat baru.

Dibawah ini edmodo.id akan memberikan contoh – contoh soal beserta pembahasannya dan juga cara menentukan persamaan pada kuadrat baru tujuannya untuk menambah wawasan dan juga pengetahuan bagi sahabat semuany.

Marilah kita simak bersama contoh – contoh soal dan juga pembahasannya yang dapat menentukan pada persamaan kuadratnya yang baru sebagai berikut yaitu.

Contoh Soal No 1

1. Di ketahui bahwa akar – akar pada persamaan kuadrat X2 + 2x + 3 = 0 ialah a dan b, sedangkan pada persamaan dari kuadratnya baru yang akar – akarnya ialah (a – 2) dan juga (b – 2) ialah ?

  • A. X2 + 6x + 5 = 0
  • B. X2 + 6x + 7 = 0
  • C. X2 + 6x + 11 = 0
  • D. X2 – 2x + 3 = 0
  • E. X2 + 2x + 11 = 0

Jawabannya : C

Pembahasannya :

Dengan berdasarkan dari persamaan kuadrat X2 + 2x + 3 = 0, dapat diketahui yaitu :

Pada jumlah akar – akar dengan persamaan kuadrat :

\[ \alpha + \beta = \frac{-b}{a} \]
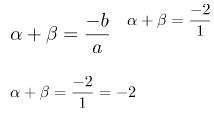
Persamaan Kuadrat Baru

Perkalian akar dengan persamaan kuadrat :

Untuk persamaan kuadratnya yang baru, maka :

Jumlah akar – akar persamaan kuadrat menjadi :

(a – 2) + (b – 2) = a + b – 4
= -2 – 4
= -6

Hasil dari perkalian akar – akar persamaan kuadrat yaitu :

(a – 2) (b – 2) = ab – 2a – 2b + 4
= ab – 2 (a + b) + 4
= 3 – 2 (–2) + 4
= 3 + 4 + 4
= 11

Jadi, dari persamaan kuadratnya yang baru pada akar – akarnya yaitu (a – 2) dan (b – 2) ialah ?

X2 – ( x1 + x2 )x + ( x1 ⋅ x2) = 0
X2 – ( -6)x + 11 = 0
X2 + 6x + 11 = 0

Selain dari cara runut yang telah kami berikan seperti di atas tadi terdapat cara yang cepat untuk menentukan persamaan kuadrat yang tujuannya untuk bentuk dari contoh soal yang seperti tadi, marilah kita simak caranya dengan langkah – langkahnya sebagai berikut.

Rumus Cepat

Perhatikan bahwasannya pada akar – akar persamaan kuadratnya yang baru ini mempunyai pengurangan terhadap nilai yang sama, yaitu -2.

Untuk menentukan persamaan dari kuadrat baru didalam kasus soal yang seperti ini yaitu dapat di lakukan dengan cara substitusi invers dan pada nilai persamaan dari kuadrat baru ke persamaan kuadrat awal, maka perhatikanlah cara – caranya sebagai berikut.

Invers dari ( X – 2) ialah ( X + 2), dengan substitusinya dengan nilai inversnya ke persamaan kuadrat awal sebagai berikiut.

( X + 2)2 + 2( X + 2) + 3 = 0
X2 + 4x + 4 + 2x + 4 + 3 = 0
X2 + 6x + 11 = 0

Hasil yang di peroleh tadi sama dengan cara sebelumnya bukan ? Akan tetapi cara cepat dapat menentukan persamaan kuadrat tersebut hanya untuk digunakan ketika akar – akar persamaan dari kuadrat baru mempunyai pengurangan maupun penjumlahannya yang sama.

Contoh Soal No 2

2. Persamaan dengan kuadrat X2 – 5x + 2 = 0 memiliki akar – akar yang diantaranya adalah a dan b, sedangkan pada persamaan kuadrat yang akar – akarnya a2 dan b2 ialah ?

  • A. X2 – 21x + 4 = 0
  • B. X2 + 21x + 4 = 0
  • C. X2 + 21x – 4 = 0
  • D. X2 – 21x – 4 = 0
  • E. – X2 – 21x + 4 = 0

Jawabannya : A

Pembahasannya :

Dengan berdasarkan persamaan kuadrat X2 – 5x + 2 = 0 dapat diperoleh dengan :

a + b = 5
a ⋅ b = 2

Sampai , jumlahan pada akar – akar yang baru :
a2 + b2 = (a + b)2 – ab
= 52 – 2(2)
= 25 – 4
= 21

Hasil dari perkalian pada akar – akar baru yaitu :
a2 ⋅ b2 = (ab)2
= 22
= 4

Sampai, pada persamaan kuaddrat barunya ialah X2 – 21x + 4 = 0.

Contoh Soal No 3

3. Apabila a dan b ini merupakan akar – akar dari persamaan kuadrat yaitu X2 – x + 3 = 0, dan pada persamaan kuadratnya yang baru maka akar – akarnya yaitu a2 – a dan b2 – b ialah ?

  • A. X2 – 6x + 9 = 0
  • B. X2 + 6x + 9 = 0
  • C. X2 + 6x – 9 = 0
  • D. X2 – 6x – 9 = 0
  • E. -X2 + 6x + 9 = 0

Jawabannya : B

Pembahasannya :

Dari persamaan kuadratnya yaitu : X2 – x + 3 = 0
a + b = 1
ab = 3

Maka jumlah pada akar – akar baru yaitu :

a2 – a + b2 – b = a2 + b2 – a – b
= (a + b)2 – 2ab  – (a + b)
= 12 – 2 ⋅ 3 – 1
= 1 – 6 – 1
= -6

Pada perkalian akar – akar baru yaitu :

(a2 – a) (b2 – b) = (ab)^{2} – ab (a + b) + ab
= 32 – 3(1) + 3
= 9

Jadi, pada persamaan kuadratnya yang baru ialah X2 + 6x + 9 = 0.

Demikianlah yang dapat edmodo.id sampaikan pada pembahasan kali ini tentang Persamaan Kuadrat Baru, semoga bermanfaat. Baca Juga :