Vektor Matematika - Pengertian, Materi, Operasi, Rumus dan Contoh Soal

Vektor Matematika – Tahukah kamu tentang vektor matematika ini ?

Ketahuilah vektor didalam ilmu matematika dan ilmu fisika itu merupakan suatu objek dari geometri yang mempunyai besaran serta arah.

Vektor juga dapat dilambangkan sbagai tanda panah seperti ini (→). Besaran suatu vektor itu proporsional yaitu dengan panjang panah dan juga arahannya yang saling bertepatan dengan arah panahnya.

Vektorpun dapat dijadikan lambang dari perpindahan sebuah titik A ke B. Tanda vektor yang sering digunakan yaitu sebagai berikut :

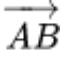
Itulah pengertian tentang vektor yang edmodo uraikan kali ini, tetapi dibawah ini ada kelengkapan dari materi vektor ini yaitu materi, operasi, rumus dan contoh soalnya.

Langsung saja disimak dibawah ini ya sahabat edmodo sekalian.

Jenis – Jenis Vektor

Dibawah ini terdapat penjelasan tentang jenis – jenis dari vektor itu sendiri, yaitu khususnya yang ada pada pelajaran matematika yang diantaranya :

Vektor Nol

Jenis vektor nol ini merupakan sebuah vektor yang memiliki nilai panjangnya yaitu nol dan dapat dinotasikan dengan {0}.

Vektor nol itu sendiri sebenarnya tidak memiliki sebuah arah vektor yang begitu jelas.

Vektor Posisi

Jenis vektor posisi ini merupakan sebuah vektor yang memiliki letak dari suatu titik yang ternyata awalnya berada dititik 0 (0,0) dan memiliki titik ujung yang berada di A(a2, a2).

Vektor Basis

Jenis vektor basis ini merupakan sebuah vektor satuan yang memiliki posisi saling tegak lurus.

Dan menurut vektor ruangnya memiliki dua dimensi yaitu (R²) dan mempunyai dua vektor basis yakni l=(1, 0) dan j=(0. 1).

Sementara didalam tiga dimensinya yaitu (R³) memiliki tiga vektor basis antaranya l=(1, 0, 0), j=(1, 0, 0), serta K=(0, 0, 1).

Vektor Satuan

Jenis vektor satuan ini merupakan sebuah vektor yang mempunyai nilai panjangnya yaitu satu satuan.

Dalam penulisan vektor satuan yang dimiliki yaitu:

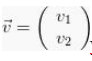
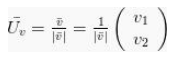
Macam – Macam Operasi Vektor

Bahwasannya vektor matematika itu tidak hanya terdiri dari jenis – jenisnya saja, tetapi vektor matematika juga memiliki beberapa macamnya juga.

Berikut ini penjelasan dari macam – macam operasi vektor :

Vektor R2

Yang dimaksud oleh macam operasi vektor R2 ini yaitu panjang sebuah segmen garisnya itu melambangkan adanya vektor dengan cara menggunakan v atau bisa juga dinotasikan dengan cara menggunakan simbol seperti |.

Dibawah ini penjelasan dari panjang sebuah vektor yakni digambarkan seperti :

Menurut panjang vektor itu sendiri ialah bentuk yang bisa saling dihubungkan dengan suatu sudut ∅ yang memang dapat dimudahkan dalam membentuk vektor beserta dengan sumbu positifnya.

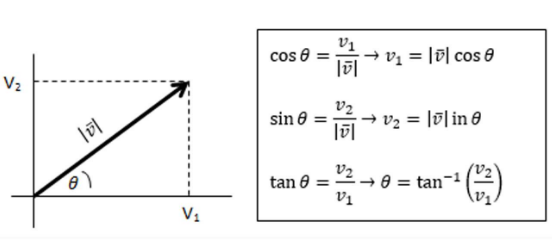
Operasi Vektor pada R2

>> Berikut ini proses penjumlahan serta pengurangan pada vektor yang terdapat di R2.

Ketahui terlebih dahulu tentang resultan. Resultan ialah sebutan dari suatu hasil yang dihasilkan dalam penjumlahan yang telah dilakukan pada kedua vektor atau bisa lebih juga.

Penjumlahan yang terjadi pada vektor tersebut juga dapatlah dilakukan dengan cara aljabar atau dapat dilakukan menggunakan cara yaitu menjumlahkan sebuah komponen yang berada tepat didalam posisi yang sama atau bisa dikatakan seletak.

Jika :

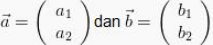
Jadi selanjutnya :

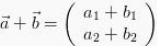
Diketahui penjumlahan menurut grafisnya sendiri itu dapatlah dilihat pada gambar yang terdapat dibawah ini, perhatikanlah :

Sedangkan pada pengurangan vektor itu ternyata diberlakukan hal yang sama pula dengan yang terjadi pada cara penjumlahannya, diantaranya yaitu sebagai berikut ini :

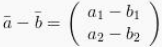
Sifat – sifat yang terdapat didalam penjumlahan vektor itu ialah seperti yang dijelaskan bawah ini, perhatikanlah :

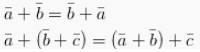
>> Rumusan pada perkalian vektor diR²itu dengan menggunakan skalar.

Sebuah vektor itu sendiri ternyata juga bisa dikalikan dengan sebuah skalar atau yang biasa disebut bilangan real yang bila dikalikan nantinya akan dapat menghasilkan sebuah vektor yang baru, tetapi itu juga apabila v merupakan vektor dan k itu merupakan skalar.

Kemudian perkalian pada vektor itu dapatlah dinotasikan sebagai contoh berikut ini:

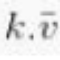
Selanjutnya dibawah ini ialah penjelasan dari beberapa keterangan yang ada, diantaranya :

Jika k>0, harusnya vektor k.v dapat searah dengan si vektor v.
Jika k<0, harusnya vektor k.v dapat berlawanan arah dengan si vektor v.
Jika k=0, harusnya vektor k.v ialah sebuah vektor identitas seperti :

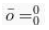
Dan apabila secara grafis perkaliannya itu dapat merubah panjang vektornya dan dapat juga dilihat pada tabel berikut ini :

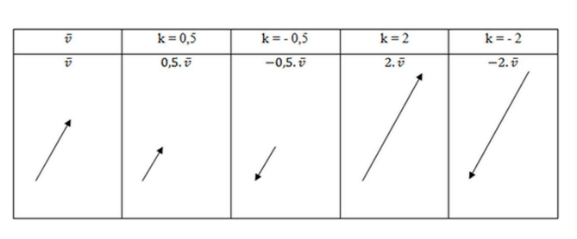
Menurut cara aljabarnya, perkalian vektor pada v bersama skalar k itu sebenarnya dapat dirumukan dengan cara menggunakan rumus seperti yang terdapat dibawah ini :

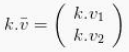
>> Perkalian pada skalar dua vektor yaitu di R² dijelaskan sebagai berikut.

Didalam sebuah perkalian skalar dua vektor itu bisa juga dinamakan sebagai dari hasil kali titik kepada dua vektor yaitu yang dapat dituliskan seperti apa yang ada dibawah ini :

Vektor R³

Vektor yang memiliki letak didalam ruang tiga dimensi yaitu x,y,z dan yang mana jarak diantara dua titik vektor itu ada didalam R³ serta bisa juga kalian ketahui dengan cara pengembangan rumus menggunakan rumus phytagoras.

Jika titik dari A(x₂.y₂.z₂) bersama B(x₂.y₂.z₂) ialah :

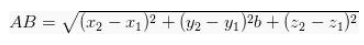
Atau pabila

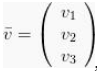
Dan akhirnya menghasilkan :

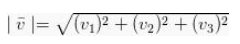
Sedangkan vektor AB itu bisa juga disebutkan kedalam dua bentuk, yaitu sebagai kolom.

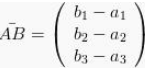
Atau bahkan didalam barisnya akan menjadi :

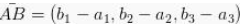
Vektor ini juga dapat disajikan menjadi kombinasi linier dari suatu vektor basis misalnya saja l(1,0,0) atau juga j(0,1,0) ataupun k(0,0,1).

Berikut ini cara penyelesaian secara lengkapnya :

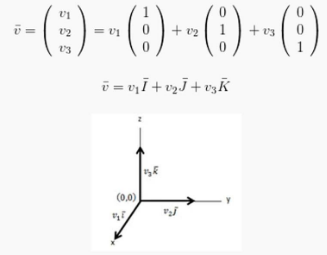
Operasi Vektor Pada R³

Operasi vektor Pada R³ ini menurut umumnya memiliki konsep yang sama pula yaitu dengan operasi yang ada pada vektor R² didalam penjumlahannya, pengurangannya, sampai ke perkaliannya juga.

Penjumlahan berserta pengurangan pada vektor di R³

Penjumlahan serta pengurangan pada vektor di R³ ini sama dengan yang terdapat pada vektor R² yaitu :

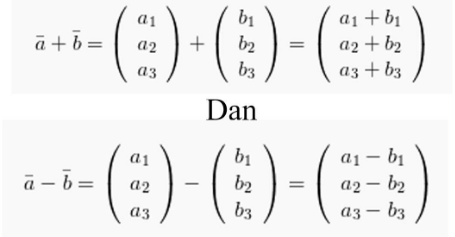
Perkalian pada vektor di R³ bersama skalar

Jika v ialah merupakan sebuah vektor dan k ialah merupakan sebuah skalar.

Maka perkalian pada vektor akan menjadi :

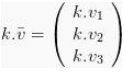
Hasil dari perkalian skalar pada dua vektor

Bukan rumus yang terdapat pada R³ saja yang ditemukan, tetapi terdapat pula rumus lain didalam hasil perkalian skalar dua vektor ini.

Jika

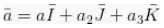
Dan jika

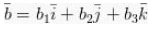
Jadi a.b ialah :

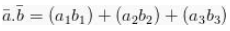
Proyeksi Orthogonal vektor

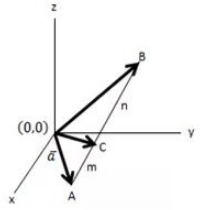
Pabila vektor ā diproyeksikan hingga menjadi vektor barb dan diberi sebutan c seperti gambar berikut ini :

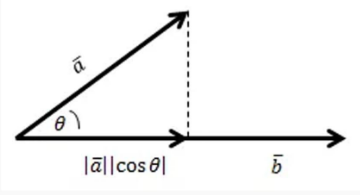
Diketahui bahwa :

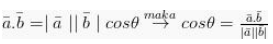
Kemudian :

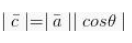
Cara mendapatkan vektornya :

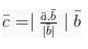
Notasi Vektor

Seperti yang sudah diterangkan diatas, bahwa vektor disini yaitu dinyatakan dengan cara mempergunakan huruf yang diberikan arah garisnya yang diatasnya.

Vektor ini juga bisa dinyatakan kedalam dua dimensi ataupun tiga dimensi bahkan lebih.

Jika dinyatakan kedalan tiga dimensi, seharusnya vektor tersebut memiliki suatu vektor satuan yang bisa dinyatakan kedalam bentuk i,j,k.

Pada vektor satuan ini ialah merupakan sebuah vektor yang besaran satu satuannya juga arahnya disesuaikan dengan sumbu yang utama, yakni seperti dibawah ini :

i ialah vektor satuan yang diarahkan searah dengan sumbu x/absis.
j ialah vektor satuan yang diarahkan searah dengan sumbu y/ordinat.
k ialah vektor satuan yang diarahkan searah dengan sumbu z/aplikat.

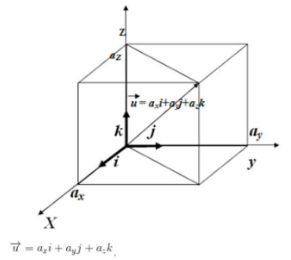
secara a_x sebagai salah satu komponen yang memilih arah kesumbu x, serta a_y merupakan komponen arah kesumbu y dan juga a_z ialah komponen arah kesumbu z.

Bentuk tulisan pada vektornya seperti dibawah ini :

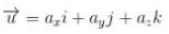
dan didalam ilmu matematikanya lebih sering dituliskan kedalam bentuk seperti dibawah ini :

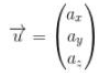
serta komponen didalam bentuk indeks angkapun bisa menjadi seperti dibawah ini :

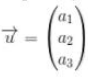
Panjang dari vektor itu dapat dituliskan seperti pada tanda mutlak dibawah ini :

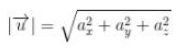
Dan didalam indeks angkanya :

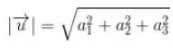
Apabila vektornya ditentukan oleh koordinatnya :

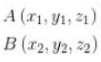
Jadi vektor AB bisa dinyatakan dengan cara :

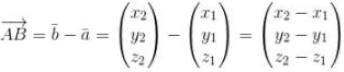
Panjang pada vektor AB

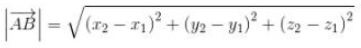
Sementara untuk suatu vektor satuan yang terdiri dari suatu vektor yang bisa dinyatakan seperti berikut ini :

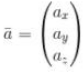
Dinyatakannya dengan :

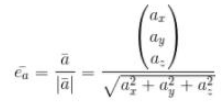
Contoh Soal Vektor Matematika

Contoh Soal 1

Jika diketahui bahwa vektor dititik A serta dititik B dan juga vektor dititik C itu terletak diantara garis Ab sama seperti dengan yang ada pada gambar dibawah ini.

Maka tentukanlah persamaan dari sebuah vektor C ini.

Jawaban :

Menurut gambar diatas itu dapat diketahui apabila :

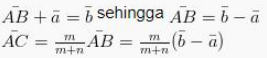
Kemudian :

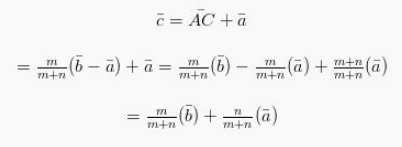
Contoh Soal 3

Apabila diketahui bahwasannya sebuah titik pada A(2,4,6), B(6,6,2), dan C(p,q,-6).

Dan jika titik A, B juga C ini terletak segaris, maka carilah berapakah nilai dari p+q tersebut ?

Jawaban :

Apabila titik titik pada A, B serta C ini segaris, maka vektor pada AB dengan vektor pada AC itu juga bisa searah atau bahkan berlainan arah.

Kemudian akan ada bilangan m yang menjadi sebuah kelipatan juga bisa membentuk sebuah persamannya misalnya seperti dibawah ini :

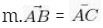
Jika B berada diantara titik A dan juga C, maka bisa didapatkan menjadai seperti dibawah ini :

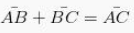
Kemudian akan bisa ddapatkan :

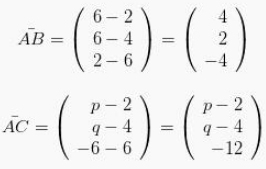
Selanjutnya bisa ditentukan kekelipatan m didalam sebuah persamaan yaitu :

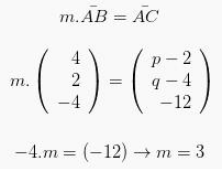
Dan hasil yang akan didapatkan yakni :

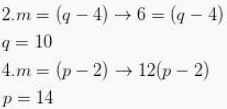
Dan bisa ditarik kesimpulan seperti : p+q=10+14=24.

Demikianlah materi vektor matematika yang dapat edmodo sampaikan kali ini.