Pertidaksamaan Nilai Mutlak

Pertidaksamaan Nilai Mutlak – Ialah merupakan pertidaksamaan yang variabelnya ada didalam tanda mutlak, dalam pertidaksamaan nilai mutlak ini dapat menyelesaikan dengan menggunakan konsep dasar dari sifat persamaan nilai mutlak tersebut.

Pengertian lain dari pertidaksamaan ialah merupakan kalimat matematika yang terbuka yang memuat ungkapan >, ≥, <, atau dengan ≤.

Sedangkan dari ketidaksamaan maupun pertidaksamaan dari mutlak (absolut) ini ialah merupakan pertidaksamaan yang selalu benar untuk disetiap nilai pengganti pada variabelnya.

Pada suatu pertidaksamaan yang selalu salah untuk setiap pengganti variabelnya itu sering disebut dengan pertidaksamaan yang palsu.

→ variabelnya ada didalam tanda mutlak | ….. |
Tanda mutlak ini selalu menghasilkan hasil yang positif, contohnya seperti : |3| = 3; |–3| = 3

Penyelesaiannya :

Apabila |x| < a artinya : –a < x < a, dimana a ≥ 0
Apabila |x| > a artinya : x < –a atau x > a, dimana a ≥ 0

Contoh Pertama :

|2x – 3| ≤ 5

Artinya :

–5 ≤ 2x – 3 ≤ 5
–5 + 3 ≤ 2x ≤ 5 + 3
–2 ≤ 2x ≤ 8

Semuanya dibagi dua :
–1 ≤ x ≤ 4

Contoh Kedua :

|3x + 7| > 2

Artinya :

3x + 7 < –2 atau dengan 3x + 7 > 2
3x < –2 – 7 atau dengan 3x > 2 – 7
x < –3 atau dengan x > –5/3

Contoh Ketiga :

|2x – 5| < |x + 4|

Kedua dari ruas tersebut dikuadratkan :

(2x – 5)2 < (x + 4)2
(2x – 5)2 – (x + 4)2 < 0
(2x – 5 + x + 4).(2x – 5 – x – 4) < 0 Ingat! a2 – b2 = (a + b) . (a – b))
(3x – 1).(x – 9) < 0

Harga pada nol yaitu : 3x – 1 = 0 atau x – 9 = 0
x = 1/3 atau x = 9

Garis pada bilangan :

Maka penyelesaiannya yaitu : {x | 1/3 < x < 4}

Contoh Keempat :
|4x – 3| ≥ x + 1

Kedua ruas dikuadratkan:

(4x – 3)2 ≥ (x + 1)2
(4x – 3)2 – (x + 1)2 ≥ 0
(4x – 3 + x + 1) . (4x – 3 – x – 1) ≥ 0
(5x – 2).(3x – 4) ≥ 0

Harga pada nol yaitu : 5x – 2 = 0 atau 3x – 4 = 0

X = 2/5 atau X = 4/3

Syaratnya :

X + 1 ≥ 0
X ≥ –1

Garis pada bilangannya.

Maka penyelesaiannya : {x | –1 ≤ x ≤ 2/5 atau x ≥ 4/3}

Contoh Kelima :

|X – 2|2 – |X – 2| < 2

Contohnya : |x – 2| = y
y2 – y < 2
y2 – y – 2 < 0
(y – 2).(y + 1) < 0

Harga pada nol yaitu : y – 2 = 0 atau y + 1 = 0
y = 2 atau y = –1

Garis pada bilangannya :

Artinya :

–1 < y < 2
–1 < |x – 2| < 2

Karena nilai mutlak pastinya bernilai positif, maka batas yang sebelah kiri tidak berlaku.

|X – 2| < 2

Sampai :

–2 < x – 2 < 2
–2 + 2 < x < 2 + 2
0 < x < 4

Sifat – Sifat Pertidaksamaan

Tanda dalam pertidaksamaan ini tidak akan berubah apabila dari kedua ruasnya ditambahkan ataupun dikurangi dengan menggunakan bilangan yang sama.

Apabila a < b maka :

A + C < B + C
A – C < B – C

Tanda dalam pertidaksamaan ini tidak akan berubah apabila dari kedua ruasnya di kali ataupun di bagi dengan menggunakan bilangan positif yang sama.

Apabila a < b, dan c ialah merupakan bilangan positif, maka :

A.C < B.C
A/B < B/C

Tanda dalam pertidaksamaan ini akan berubah apabila dari kedua ruasnya pada pertidaksamaannya di kali ataupun di bagi dengan menggunakan bilangan negatif yang sama.

Apabila a < b, dan c ialah merupakan bilangan negatif, maka :

A.C > B.C
A/C > B/C

Tanda dalam pertidaksamaan ini tidak akan berubah apabila dari kedua ruasnya dari positif masing – masing di kuadratkan.

Apabila a < b; a dan b sama – sama positif, maka : a2 < b2.

Pertidaksamaan Kuadrat

→ Variabelnya berpangkat 2

Penyelesaiannya :

Ruas sebelah kanannya di buat menjadi nol
Dan difaktorkan

Tentukanlah harga nol, yaitu dengan nilai variabel yang menyebabkan nilai faktor sama dengan nol.

Gambarkanlah garis bilangannya.

Apabila tanda pertidaksamaannya ≥ ataupun ≤, maka harga nol ditandai dengan tanda titik hitam •
Apabila tanda pertidaksamaannya > ataupun <, maka harga nol ditandai dengan tanda titik putih °

Tentukanlah tanda (+) ataupun (–) pada masing – masing intervalnya di garis bilangan, caranya ialah dengan memasukkan salah satu dari bilangan pada interval tersebut pada persamaan di ruas kiri.
Tanda pada garis bilangannya berselang – seling, kecuali apabila ada batas dari rangkap (harga nol yang muncul dua kali ataupun sebanyak dari bilangan genap untuk pertidaksamaan tingkat tinggi, dari batas rangkap tidak dapat merubah tanda.

Tentukanlah himpunan penyelesaiannya

→ Apabila tanda pertidaksamaan > 0 artinya daerah pada garis bilangan yang diarsirkan ialah yang bertanda (+)
→ Apabila tanda pertidaksamaan < 0 artinya daerah pada garis bilangan yang diarsirkan ialah yang bertanda (–)

Contohnya :

(2x – 1) 2 ≥ (5x – 3) . (x – 1) – 7
4×2 – 4x + 1 ≥ 5×2 – 5x – 3x + 3 – 7
4×2 – 4x + 1 – 5×2 + 5x + 3x – 3 + 7 ≥ 0

–x2 + 4x + 5 ≥ 0
–(x2 – 4x – 5) ≥ 0
–(x – 5) . (x + 1) ≥ 0

Harga dari nol : x – 5 = 0 atau x + 1 = 0
x = 5 atau x = –1

Garis bilangannya :

Dengan menggunakan titik hitam karena ada tanda dari pertidaksamaan ≥
apabila dimasukkan x = 0 maka hasilnya positif.

Karena 0 ini berada di antara –1 dan 5, maka dari daerah tersebut bernilai positif, di sebelah kiri dan juga kanannya bernilai negatif.

Karena tanda dari pertidaksamaan ≥ 0, maka yang diarsirkan ialah yang tandanya positif.

Maka penyelesaiannya yaitu : {x | –1 ≤ x ≤ 5}

Pertidaksamaan Tingkat Tinggi

→ Variabel yang berpangkat lebih dari dua

Penyelesaiannya sama dengan pertidaksamaan kuadrat.

Contohnya :
(2x + 1)2 . (x2 – 5x + 6) < 0
(2x + 1)2 . (x – 2) . (x – 3) < 0

Harga dari nol yaitu : 2x + 1 = 0 ataupun x – 2 = 0 atau x – 3 = 0

X = –1/2 atau X = 2 atau X = 3

Garis dari bilangannya :

Harus menggunakan titik putih karena tanda dari pertidaksamaan <
Apabila dimasukkan X = 0 maka hasilnya positif.
Karena 0 berada di antara –1/2 dan 2, maka dari daerah tersebut nilainya positif.
Karena –1/2 ialah batas rangkap (–1/2 yang muncul sebanyak dua kali sebagai harga nol, jadi –1/2 ini merupakan batas rangkap), maka dari sebelah kiri –1/2 ini juga nilainya positif.
Selain dari daerah yang dibatasi oleh batas rangkap, maka tanda positif dan juga negatifnya berselang – seling.
Karena dari tanda pertidaksamaan ³ 0, maka yang dapat diarsirkan ialah merupakan nilai yang positif.

Maka penyelesaiannya : {x | 2 < x < 3}

Pertidaksamaan Pecahan

→ Ada pembilang dan juga penyebutnya.

Penyelesaiannya :

Ruas yang sebelah kanan maka di jadikan nol.
Samakan dengan penyebutnya dari ruas sebelah kiri.
Faktorkan pembilang dan juga penyebutnya, jika bisa.
Carilah nilai – nilai dari variabel yang menyebabkan pembilang dan juga penyebutnya sama dengan nol maka harga nol tersebut untuk pembilang dan juga penyebutnya.
Gambarlah garis bilangan yang dapat memuat semua nilai yang di dapatkan pada langkah empat.
Apapun tanda dari pertidaksamaannya, harga nol untuk penyebutnya selalu digambarkan dengan titik putih dan pada penyebut suatu pecahan tidak boleh sama dengan nol supaya pecahan tersebut memiliki nilai.

Tentukanlah tanda (+) ataupun (–) pada masing – masing intervalnya.

Contoh Pertama :

Harga dari nol pada pembilang : –5x + 20 = 0
–5x = –20 → x = 4

Harga dari nol pada penyebut : x – 3 = 0 → x = 3

Garis bilangannya :

→ X = 3 maka digambar dengan menggunakan titik putih karena merupakan nol untuk penyebutnya.

Contoh Kedua :

Harga dari nol pada pembilang : x – 2 = 0 ataupun x + 1 = 0
x = 2 atau x = –1

Harga dari nol pada penyebut : tidak ada, karena penyebut tidak bisa difaktorkan dan apabila dihitung nilai diskriminannya maka :
D = b2 – 4 . a . c = 12 – 4 . 1 . 1 = 1 – 4 = –3

Nilai D nya ialah negatif, sampai persamaan tersebut tidak memiliki akar yang real.

Catatan : Apabila nilai D nya tidak negatif, maka gunakanlah rumus abc untuk mendapatkan harga nol nya.
Garis pada bilangan :

Maka penyelesaiannya : {x | x ≤ –1 ataupun x ≥ 2}

Pertidaksamaan Irasional Atau Pertidaksamaan Bentuk Akar

→ Variabelnya berada didalam tanda akarnya.

Penyelesaiannya :

Kedua ruas nya harus dikuadratkan.
Jadikan ruas sebelah kanan sama dengan nol.
Selesaikan seperti menyelesaikan pertidaksamaan linear ataupun kuadrat.
Syarat tambahan : Yang ada di setiap tanda akar harus ≥ 0

Contoh Pertama :

Kuadratkanlah kedua ruas tersebut :

x2 – 5x – 6 < x2 – 3x + 2
x2 – 5x – 6 – x2 + 3x – 2 < 0
–2x – 8 < 0

Semuanya dikali dengan –1 :

2x + 8 > 0
2x > –8
X > –4

Syarat Pertama :

x2 – 5x – 6 ≥ 0
(x – 6) . (x + 1) ≥ 0

Harga nol yaitu : X – 6 = 0 atau X + 1 = 0
X = 6 atau X = –1

Syarat Kedua :

x2 – 3x + 2 ≥ 0
(x – 2) . (x – 1) ≥ 0

Harga nol yaitu : X – 2 = 0 atau X – 1 = 0
X = 2 ataupun X = 1

Garis pada bilangannya :

Maka penyelesaiannya : {x | –4 < x ≤ –1 atau x ≥ 6}

Contoh Kedua :

Kuadratkanlah kedua ruas tersebut :

x2 – 6x + 8 < x2 – 4x + 4
x2 – 6x + 8 – x2 + 4x – 4 < 0
–2x + 4 < 0
–2x < –4

Semuanya dikalikan dengan –1
2x > 4
X > 2

Syaratnya :

x2 – 6x + 8 ≥ 0
(x – 4) . (x – 2) ≥ 0

Harga nol yaitu : X – 4 = 0 atau X – 2 = 0
X = 4 atau X = 2

Garis pada bilangannya :

Maka penyelesaiannya yaitu : {x | x ≥ 4}

Pertidaksamaan dari mutlak ini sering disebut dengan ketidaksamaan dan tentunya pada ketidaksamaan ini merupakan sebuah kalimat matematika yang tertutup.

Demikian juga untuk kalimat yang terbuka P(x) ≤ Q(x) ialah merupakan ekuivalen dengan kalimat – kalimat yang terbuka dari bentuk A sampai bentuk E dengan mengganti < atau > dengan ≤ atau ≥ dengan syarat yang sama juga, yaitu R(x) > 0 dan R(x) < 0 seperti yang di atas.

Contoh Soal

1. Carilah himpunan penyelesaiannya dari pertidaksamaan | X + 1 | < 3 ialah ?

Jawabannya :

2. Selesaikanlah dari pertidaksamaan | X + 3 | < 2 – X ialah ?

Jawabannya :

3. Carilah himpunan penyelesaiannya dari pertidaksamaan harga mutlak | X – 5 | ≤ 4 ialah ?

Jawabannya :

4. Carilah himpunan penyelesaiannya | X² – 10 | < 6

Jawabannya :

Cara Yang Pertama :

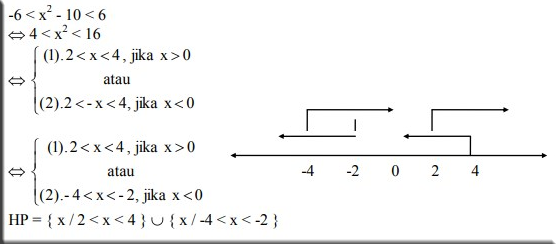
Cara Yang Kedua :

5. Buktikanlah bahwa untuk setiap X, Y, Z ∈ R berlaku | X – Y| ≤ | X – Z | + | Z – Y | ialah ?

Jawabannya :

Demikianlah yang dapat edmodo.id sampaikan pada ulasan kali ini tentang Pertidaksamaan Nilai Mutlak. Baca Juga : Limit Tak Hingga – Pengertian, Fungsi, Rumus Dan Contoh Soal