Pertidaksamaan ialah merupakan suatu bentuk atau kalimat matematis yang memuat tanda lebih dari ” > “, kurang dari ” < “, lebih dari atau sama dengan “≥ “, dan kurang dari atau sama dengan ” ≤ “.
Maka dari itu, linear dapat kita artikan sebagai suatu bentuk dari aljabar dengan variabel yang pangkatnya tertinggi ialah 1, Dibawah ini kami akan menjelaskan tentang contoh penerapan pertidaksamaan linear.
Pertidaksamaan Linear Satu Variabel

Sebalumnya kalian telah mempelajari tentang pertidaksamaan linear kali ini kita akan mempelajari pertidaksamaan linear satu variabel.
Namun pertidaksamaan linear satu variabel ini merupakan sautu bentuk pertidaksamaan dengan memuat satu variabel dengan pangkat yang tertinggi ialah 1 linear.
Dibawah ini merupakan bentuk umum dari pertidaksamaan linear satu variabel yaitu sebagai berikut.
Bentuk Umum Pertidaksamaan Linear Satu Variabel
- AX+ b > c
- AX + b < c
- AX + b ≥ c
- AX + b ≤ c
Keterangannya :
- A : Koefisien variabel x
- X : Variabel
- B, C : Konstanta
- <, >, ≤, ≥ : Tanda pertidaksamaan
Pertidaksamaan Linear Dua Variabel
Pada sebelumnya kalian telah mempelajarinya tentang pertidaksamaan linear dua variabel, namun pada kali ini kita akan membahas tentang pertidaksamaan linear dua variabel.
Namun pada pertidaksamaan linear dua variabel ini ialah bentuk dari pertidaksamaan yang telah dimuat dua variabel dengan pangkat yang tertinggi yaitu variabel ialah 1.
Bentuk Umum Pertidaksamaan Linear Dua Variabel
- AX + by > c
- AX + by < c
- AX + by ≥ c
- AX + by ≤ c
Keterangannya :
- X, Y : Variabel
- A : Koefisien variabel x
- B : Koefisien variabel y
- C : Konstanta
- <, >, ≤, ≥ : Tanda pertidaksamaan
Sistem Pertidaksamaan Linear
Apa yang kalian ketahui tentang perbedaan dari pertidaksamaan linear dan juga sistem pertidaksamaan linear ? Perbedaan dari keduanya tersebut terletak pada banyaknya pertidaksamaan.
Namun pada sistem pertidaksamaan linear, contohnya pada sistem pertidaksamaan linear dua variabel ini terdapat lebih dari satu pertidaksamaan linear dua variabel supaya dapat membuat model matematika dan dapat ditentukan solusinya.
Sistem Pertidaksamaan Linear Dua Variabel
Apa yang telah disebutkan pada sebelumnya, sistem pertidaksamaan linear dua variabel ini mempunyai beberapa pertidaksamaan linear dua variabel supaya dapat ditentukan solusi dari pertidaksamaan tersebut.
Perhatikanlah contoh di bawah ini untuk menentukan solusinya dari sistem pertidaksamaan linear dua variabel.
Contohnya terdapat didalam sistem pertidaksamaan linear dua variabel yaitu sebagai berikut.
3x + 2y < 8
X + Y < 3
Tentukanlah suatu daerah penyelesaian dari sistem pertidaksamaan linear dua variabel tersebut apabila X dan Y ini merupakan suatu bilangan bulat yang positif.
Pembahasannya :
Model matematika :
3x + 2y < 8
X + Y < 3
Dengan menggunakan sebuah grafik ini, dapat dibuat garis 3x + 2y = 8, namun kemudian dapat ditentukan bagian yang merupakan 3x + 2y < 8.
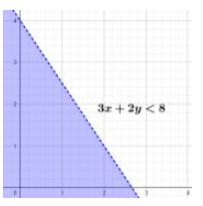
Dengan menggunakan sebuah grafik ini, dapat dibuat garis x + y = 3, namun kemudian dapat ditentukan bagian yang merupakan x + y < 3.
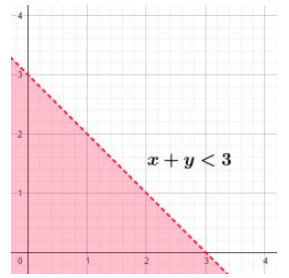
Dan kemudian tentukanlah titik potong dari kedua garis tersebut yaitu.
3x + 2y = 8
X + Y = 3
Dengan menggunakan metode eliminasi ini dapat diperoleh dengan :
3x + 2y = 8
2x + 2y = 6
————– –
X = 2
Substitusikan nilai x = 2 ke persamaan x + y = 3
2 + y = 3
y = 3 – 2
Y = 1
Maka Titik potong dari kedua garis tersebut ialah (2, 1).
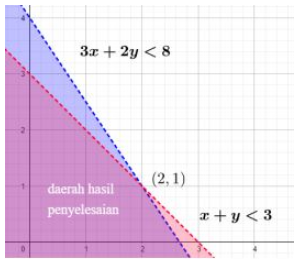
Daerah yang berwarna ungu ini merupakan suatu daerah dan hasil penyelesaiannya pada sistem pertidaksamaan linear dua variabel.
Pelajarilah contoh soal yang ada di bawah ini untuk meningkatkan lagi pemahaman anda.
Contoh Soal Pertidaksamaan Linear
1. Tentukanlah solusi dari pertidaksamaan linear sebagai berikut ini untuk nilai variabel yang merupakan suatu bilangan bulat yang positif.
- 3x < 12
- 2y > 6
Pembahasannya :
- 3x < 12
- X < 12/3
- X < 4
Solusinya : {1, 2, 3}
- 2y > 6
- Y > 6/2
- Y > 3
Solusinya : {4, 5, 6, . . .}
2. Tentukanlah daerah penyelesaiannya dari sistem pertidaksamaan linear dua variabel sebagai berikut.
4x + 2 y < 12
2x + 3y < 10
Pembahasannya :
Buatlah garis 4x + 2y = 12 dan tentukanlah daerah yang menunjukkan 4x + 2y < 12.
Buatlah garis 2x + 3y = 10 dan tentukanlah daerah yang menunjukkan 2x + 3y < 10.
Tentukanlah titik potong dari kedua garis.
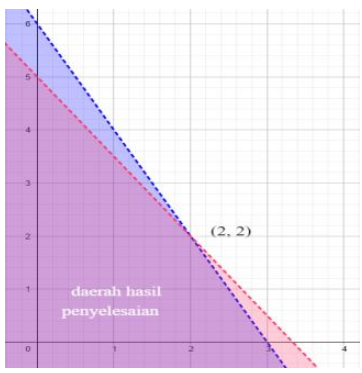
Daerah hasil penyelesaian yang merupakan daerah yang warnanya ungu.
Pertidaksamaan Rasional
Pertidaksamaan rasional ini merupakan kalimat matematika yang terbuka dan dapat menggunakan dengan suatu tanda > (lebih dari), < (kurang dari) ≤ (kurang dari atau sama dengan) dan ≥ (lebih dari atau sama dengan).
Pertidaksamaan rasional ialah merupakan suatu bentuk dari pertidaksamaan yang memuat fdari ungsi rasional, yang mana fungsi tersebut dapat dinyatakan didalam bentuk f(x)/g(x) dengan syarat g(x) ≠ 0.
Bentuk – Bentuk Umum Pertidaksamaan Rasional
Dibawah ini ada beberapa bentuk umum dari pertidaksamaan rasional yaitu sebagai berikut :
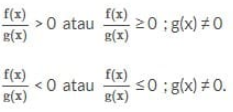
Langkah Penyelesaiannya :
Didalam proses ini merupakan penyederhanaan dan bentuk pertidak samaan pada rasional ini, dibawah ini ada beberapa macam yang tidak dapat dibenarkan dan kalian perlu memperhatikan sebabnya yang dapat merubah domain fungsinya sendiri dengan hal – halnya tersebut yang meliputi yaitu sebagai berikut :
- Kali Silang
Kali silang yang dimaksud yaitu :
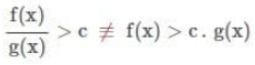
- Mencoret fungsi maupun faktor yang sama pada pembilang dan juga penyebutnya
Didalam hal ini kita tidak dapat membenarkannya untuk mencoret fungsinya maupun faktor yang sama pada pembilang dan juga penyebutnya, yaitu :
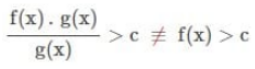
Untuk menyelesaikan sebuah himpunan pertidak samaan rasional ini dapat ditentukan dengan cara langkah – langkah sebagai berikut yaitu :
- Himpunan dapat nyatakan kedalam bentuk umum.
- Tentukanlah pembuat nolnya pada pembilang dan juga penyebutnya.
- Tulislah terlebih dulu untuk membuat nol pada garis bilangan, dan tentukan juga tandanya untuk tiap – tiap interval pada garis bilangan tersebut.
- Tentukanlah daerah penyelesaiannya yaitu pertidak samaan “>” atau “≥” degan daerah penyelesaiannya yang berada pada interval dan bertanda positif untuk pertidak samaan “<” atau “≤” dengan daerah penyelesaianya yang berada pada interval yang bertanda negaitf.
- Dengan memperhatikan suatu syarat bahwa penyebut tidak sama dengan nol, tulislah himpunan penyelesaiannya yaitu interval yang dapat memuat daerah penyelesaiannya.
Contoh Soal
Setelah kita memahami beberapa dari keterangan tadi, namun sekarang kita dapat mencoba untuk membahas contoh soalnya sebagai berikut supaya kita dapat lebih memahami lagi :
Contoh Soal :
1. Tentukanlah himpunan penyelesaian dari :
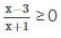
Jawabannya :
Membuat nol yaitu
X − 3 = 0 ⇒ x = 3
X + 1 = 0 ⇒ x = −1
Syaratnya :
X + 1 ≠ 0 ⇒ x ≠ −1

Sebab dari pertidak samaan yang tandanya “≥”, maka daerah penyelesaiannya berada pada interval yang tandanya positif (+).
Yaitu : Himpunan = {X < −1 atau X ≥ 3}
Pertidaksamaan Kuadrat
Bentuk umum dari pertidak samaan kuadrat yaitu sebagai berikut :
Ax² + bx + c > 0
Ax² + bx + c ≥ 0
Ax² + bx + c < 0
Ax² + bx + c ≤ 0
A, B, C bilangan real dan a ≠ 0.
Langkah – Langkah Penyelesaian
Dari himpunan penyelesaian pada pertidak samaan kuadrat dapat ditentukan dengan langkah – langkah dibawah ini yaitu :
Langkah Pertama
Tentukanlah mebuat nol dengan cara merubah tanda pertidak samaannya sampai menjadi (=). Dan pada akar – akar persamaan kuadrat yang didapat yaitu pembuat nol.
x2 + x – 6 = 0 ,difaktorkan
menjadi (x +3)(x-2) = 0
Pembuat nol dari persamaan tersebut dapat dicari dengan pakai cara ini.
Yang pertama gunakanlah :
X + 3 = 0
X = -3
Yang kedua gunakanlah :
X – 2 = 0
X = 2
Jadi, pembuatan nolnya sudah didapatkan yaitu -3 dan 2.
Langkah Yang Kedua
Gambarkanlah pembuat nol pada garis bilangan, kemudian tentukanlah tandanya masing – masing interval dengan cara mensubstitusikan sembarang bilangan yang ada di tiap interval ke persamaan pada ruas kiri.
Tulislah (+) ada hasil dari substitusi ialah yang bernilai positif dan tulislah (−) apabila hasil dri substitusi ialah bernilai negatif.
Catatan :
Tiap – Tiap internal terdapat tandanya yaitu selalu selang – seling (+)(−)(+) atau (−)(+)(−), kecuali apabila akar – akar yang didapat sama atau disebut kembar.
Tipsnya :
Apabila akar – akar yang didapat berbeda, cukuplah cari tandanya pada satu interval saja, yang sisanya tinggal ditulis berselang – seling untuk mengikuti pola diatas.
Dan dahulukan interval yang memuat angka nol supaya perhitungannya lebih mudah apabila nol bukan merupakan pembuat nol.
Langkah Yang Ketiga
Tentukanlah pada daerah penyelesaian maupun arsiran.
pertidak samaan “>” atau “≥”, daerah penyelesaian yang berada pada interval yang tandanya positif (+).
Pertidak samaan “<” atau “≤”, daerah penyelesaian yang berada pada interval yang tandanya negatif (−).
Langkah Yang Keempat
Tulislah suatu himpunan penyelesaian, yaitu interval yang dapat memuat daerah penyelesaian.
Himpunan penyelesaian ada pada ujung – ujung interval.
Contoh Soal
Contoh Soal Pertama
Tentukanlah Himpunan dari −x² − 3x + 4 > 0
Jawabannya :
Pembuat nol
−x² − 3x + 4 = 0
x² + 3x − 4 = 0
(x+4) (x−1) = 0
X = −4 atau x = 1
Untuk interval −4 < x < 1, ambil x = 0
−x² − 3x + 4 = −(0)² − 3(0) + 4 = 4 (+)

Karena dari pertidak samaan bertanda “>” , maka daerah penyelesaian ada pada interval yang tandanya (+).
= Himpunan = {−4 < x < 1}
Contoh Soal Yang Kedua
Tentukanlah Himpunan dari x² − 2x − 3 ≥ 0
Jawabannya :
Pembuat nol
x² − 2x − 3 = 0
(x+1) (x−3) = 0
X = −1 atau x = 3
Untuk interval −1 < x < 3, ambil x = 0
x² − 2x − 3 = (0)² − 2(0) − 3 = −3 (−)
Karena pertidak samaan bertanda “≥” , maka, daerah penyelesaian ada pada interval yang tandanya (+).
= Himpunan = {x ≤ −1 atau x ≥ 3}
Contoh Soal Yang Ketiga
X(3x + 1) < (x + 1)² − 1
Jawabannya :
Ubahlah terlebih dulu ke dalam bentuk umum pada pertidak samaan kuadrat yaitu :
X (3x + 1) < (x + 1)² − 1
⇔ 3x² + x < x² + 2x + 1 − 1
⇔ 2x² − x < 0
Pembuat nol :
2x² − x = 0
X ( 2x − 1 ) = 0
X = 0 atau x = 1/2
Untuk interval X > 1/2 maka ambil X = 1
2x² − x = 2(1)² − 1 = 1 (+)

Maka karena pertidak samaan bertanda “<” , maka, pada daerah penyelesaian ada di interval yang tandanya (−).
= HP = {0 < x < 1/2}
Pertidaksamaan Akar
Pertidak samaan akar (irasional) ialah merupakan suatu bentuk dari pertidak samaan yang fungsi – fungsi pembentuknya berada dibawah tanda akarnya, baik itu fungsi pada ruas kiri, ruas kanan maupun pada kedua ruasnya.
Atau sering disebut dengan dengan bilangan real, pertidakasamaan akar ini apabila didefinisikan maka syarat pada akarnya terpenuhi yaitu fungsi yang berada dibawah tanda akar yang bernilai lebih atau sama dengan nol.
Penyelesaian dari pertidaksamaan irasional ini dilakukan dengan cara menguadratkan pada kedua ruas dan dengan kemudian disederhanakan dengan operasi – operasi aljabar sampai diperoleh suatu interval yang tertentu, dan pada solusi akhirnya ialah irisan dari syarat akar dengan interval yang telah diperoleh tadi.
Bentuk Pertidaksamaan Irasional
1. Bentuk √f(x)>kf(x)>k
Untuk K ≥ 0
Solusinya : f(x) ≥ 0 ∩ f(x) > k2
Untuk K < 0
Solusinya : f(x) ≥ 0
Contoh Yang Pertama
Tentukanlah Himpunan dari √x−2>3x−2>3
Jawabannya :
X − 2 ≥ 0 ∩ x − 2 > 32
X ≥ 2 ∩ x > 11
⇒ X > 11
Himpunan = {x > 11}
ContohYang Kedua
Tentukanlah Himpunan dari √x+3>−2x+3>−2
Jawabannya :
X + 3 ≥ 0
⇒ X ≥ −3
Himpunan = {x ≥ −3}
2. Bentuk dari √f(x)<kf(x)<k
Solusinya : f(x) ≥ 0 ∩ f(x) < k2
Bentuk dari diatas tadi hanya memiliki solusi apabila K > 0. Jika k ≤ 0, maka pada pertidak samaan diatas tidak memiliki solusi atau penyelesaiannya.
Pertidaksamaan Pecahan
Penyelesaian maupun himpunan penyelesaian dari pertidak samaan bentuk pecahan dapat dapat ditentukan dengan menggunakan garis bilangan.
Sebagai contohnya, penyelesaian pada pertidak samaan pecahan berikut ini.
X – 1 < 0
X – 2
Bisa ditentukan dengan melalui langkah – langkah yaitu sebagai berikut.
Langkah Yang Pertama
Nilai nol bagian pembilang : x – 1 = 0 ⇒ x = 1 Nilai nol bagian penyebut : x – 2 = 0 ⇒ x = 2
Langkah Yang Kedua
Nilai nol pada pembilang dan juga penyebut dapat ditempatkan pada diagram garis bilangan contohnya seperti yang telah ditunjukkan pada gambar berikut ini.

Nilai – Nilai nol tersebutmembagi garis bilanyangan menjadi tiga interval, yaitu X < 1, 1 < X < 2, dan X > 2.
Nah inilah yang dapat edmodo.id sampaikan pada pembahasan tentang pertidaksamaan, semoga apa yang telah kita sampaikan ini dapat bermanfaat untuk kalian semua.
Baca Juga :
