Persamaan Trigonometri - Bentuk, Contoh Soal dan Cara Penyelesaiannya

Apa yang dimaksud dengan Persamaan trigonometri? pengertian dari persamaan trigonometri sendiri ialah merupakan suatu persamaan yang didalamanya mencakup fungsi trigonometri berdasarkan dari suatu sudut yang belum diketahui.

Contoh persamaan trigonometri adalah:

2 sin x = 1cosx = – ½
Cara penyelesaian mengenai persamaan trigonometri sendiri ialah dengan mencari setiap sudut x sehingga bisa menentukan persamaan tersebut bisa menjadi benar.

Kemudian jika ingin menyelesaikan atas persamaan trigonometri ini, maka kita bisa menerapkan sebuah operasi aljabar dan juga identitas trigonometri apabila dibutuhkan.

Di bawah ini sedikit kami singgung terkait mengenai cara umum untuk menyelesaikan materi persamaan trigonometri.

Yang mana pada umumnya Persamaan trigonometri ini dibedakan atas dua bentuk, yang diantaranya adalah.

Menggunakan kalimat terbuka
Berbentuk identitas.

Cara untuk menyelesaikan materi persamaan trigonometri yang dijadikan kedalam bentuk kalimat terbuka, artinya pengerjaan harus menentukan nilai variabel yang ada terlebih dahualu dari persamaan tersebut hingga nilai dari persamaan itu benar.

Rumus Trigonometri

Secara umum terdapat tiga jenis rumus periode yang biasanya kerap digunakan guna menyelesaikan persamaan trigonometri ini, yang diantaranya adalaha:

sin x
Yang pertama adalah sin α maka x = α + k.360 dan x
= (180 – α) + k.360

cos x
Yang kedua adalah cos α maka x
= α + k.360
dan x = – α + k.360

tan x
Yang ketiga adalah tan α maka x = α + k.180

Jadi k disini merupakan bilangan bulat

Contoh Soal Persamaan Trigonometri

Di bawah sudah edmodo.id sajikan beberapa soal latihan untuk menyelesaikan persamaan trigonometri, yakni sebagai berikut.

Contoh soal 1

Pada 0^o ≤ x ≤ 360^o maka coba tentukanlah cara untuk menyelesaikan himpunan dari : sin 3x = 1/2

Jawab :
sin 3x = 1/2
sin 3x = sin 30^o

3x = 30^o + n.360^o
x = 10^o + n.120^o
Jika n = 0 dan x = 10^o
Jika n = 1 dan x =130^o
Jika n = 2 dan x =250^o

3x = 180^o – 30^o + n.360^o
x = 50^o + n.120^o
Kemudian jika untuk n = 0 maka x = 50^o
Jika untuk n = 1 dan x = 170^o
Jika untuk n = 2 dan x = 290^o

Maka, untuk menyelesaikan himpunan diatas ialah seperti berikut
{10^o, 50^o, 130^o, 170^o, 250^o, 290^o}

Contoh soal 2

Berikutnya jika untuk 0^o ≤ x ≤ 180^o maka untuk menyelesaikan himpunan dari cos 5x = 1/2 √2

Jawab :
cos 5x = 1/2 √2
cos 5x = cos 45^o

5x = 45^o + n.360^o
x = 9^o + n.72^o
Kemudian jika untuk n = 0 maka x =9^o
Jika untuk n = 1 dan x =81^o
Jika untuk n = 2 dan x =153^o

5x = -45^o+n.360^o
x= -9^o + n.72^o
Kemudian untuk n= 1 maka x = 63^o
Jika untuk n = 2 maka x = 135^o

Maka, bentuk himpunan dari penyelesaiannya ialah sebagai berikut.
{9^o, 63^o, 81^o, 135^o, 153^o}

Contoh soal 3

Tentukanlah Himpunan apabila persamaan tan 4x = √3 0^o ≤ x ≤ 360^o dan penyelesaiannya adalah….

Jawab :

tan 4x = √3
tan 4x = tan 60^o
4x = 60^o + n.180^o
x = 15^o + n.45^o

jadi n = 0 dan x = 15^o
jadi n = 1 dan x = 60^o
jadi n = 2 danx = 105^o
jadi n = 3 danx = 150^o
jadi n = 4 dan x = 195^o
jadi n = 5 dan x = 240^o
jadi n = 6 dan x = 285^o
jadi n = 7 dan x = 330^o

Maka, penyelesaian dari pada himpunan ini ialah
{15^o, 60^o, 105^o, 150^o, 195^o, 240^o, 285^o, 330^o}

Contoh soal-4

Berikut ini tentukanlah himpunan agar dapat menyelesaikan dari pada persamaan sin 3x =cos 2x dan 0^o ≤ x ≤ 360^o ?…

Jawab :

sin 3x = cos 2x
sin 3x = sin (90^o – 2x)

3x = 90^o – 2x + n.360^o
5x = 90^o + n.360^o
x = 18^o + n.72^o

Jadi n = 0 dan x = 18^o
Jadi n = 1 dan x = 90^o
Jadi n = 2 dan x = 162^o
Jadi n = 3 dan x = 234^o
Jadi n = 4 dan x = 306^o

3x = 180^o – (90^o – 2x) + n.360^o
3x = 90^o + 2x + n.360^o
x = 90^o + n.360^o
Jadi n = 0 maka x = 90^o

Maka, untuk penyelesaiannya ialah seperti berikut:
{18^o, 90^o, 162^o, 234^o, 306^o}

Contoh Soal5

Apabila sudah diketahui bahwa persamaan dari pada sin 5x + sin 3x = cos x
dan 0^o ≤ x ≤ 360^o . maka tentukanlah himpunan berikut untuk menyelesaikannya …

Jawab :

sin 5x + sin 3x = √3 cos x
2 sin 1/2 (5x + 3x) cos 1/2 (5x – 3x) = √3 cos x
2 sin 4x cos x = √3 cos x
2 sin 4x cos x – √3 cos x = 0
cos x ( 2 sin 4x – √3) = 0
cos x = 0 atau sin 4x = 1/2 √3

cos x = 0
cos x = cos 90^o

x = 90^o + n.360^o
jadi n = 0 maka x = 90^o

x = -90^o + n.360^o
jadi n = 1 dan x = 270^o

sin 4x = 1/2 √3
sin 4x = sin 60^o

4x = 60^o + n.360^o
x = 15^o + n.90^o

jadi n = 0 dan x = 15^o
jadi n = 1 dan x = 105^o
jadi n = 2 dan x = 195^o
jadi n = 3 dan x = 285^o

4x = 180^o – 60^o + n.360^o
4x = 120^o + n.360^o
x = 30^o + n.90^o

jadi n = 0 dan x = 30^o
jadi n = 1 dan x = 120^o
jadi n = 2 dan x = 210^o
jadi n = 3 dan x = 300^o

Maka, penyelesaiannya ialah sebagai berikut

{15^o, 30^o, 90^o, 105^o, 120^o, 195^o, 210^o, 270^o, 285^o, 300^o}

Contoh Soal 6

Tentukanlah Himpunan dari pada penyelesaian atas persamaan
√3 tan² 2x – 4tan 2x + √3 = 0 dan juga 0^o ≤ x ≤ 360^o ialah…

Jawab :

√3 tan² 2x – 4tan 2x + √3 = 0

Agar bisa lebih mudaha menyelesaikannya himpunan ini, maka kita bisa menggunakan rumus ABC sebagai berikut

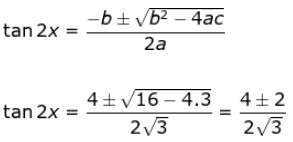
Kemungkinan 1 :

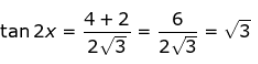
tan 2x = tan 60^o
2x = 60^o + n.180^o
x = 30^o + n.90^o

jadi n = 0 dan x = 30^o
jadi n = 1 dan x = 120^o
jadi n = 2 dan x = 210^o
jadi n = 3 dan x = 300^o

Kemudian Kemungkinan lainnya :

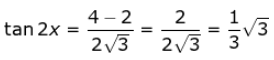
tan 2x = tan 30^o
2x = 30^o + n.180^o
x = 15^o + n.90^o

jadi n = 0 dan x = 15^o
jadi n = 1 dan x = 105^o
jadi n = 2 dan x = 195^o
jadi n = 3 dan x = 285^o

Maka, penyelesaiannya dari pada himpunan diatas ialah?

{15^o, 30^o, 105^o, 120^o, 195^o, 210^o, 285^o, 300^o}

Sekian yang dapat kami sampaikan terkait mengenai persamaan trigonometri, semoga ulasan ini dapat bermanfaat untuk sahabat semua.