Limit Tak Hingga – Apa sajakah yang sudah kalian ketahui mengenai pembahasan limit tak hingga ini ?
Kali ini edmodo akan menyampaikan sebuah ulasan materi tentang limit tak hingga ini lengkap dengan pengertian, materi, rumus dan contoh Soalnya.
Langsung saja disimak ulasan pertama tentang pengertian dari limit tak hingga ini sebagai berikut.

Limit tak hingga ialah kajian yang tepat dalam mengetahui kecendrungan suatu fungsi apabila nilai variabelnya dibuat semakin besar.
Apabila di katakan, x menuju tak hingga, ditulis x → ∞, artinya nilai x semakin besar atau bertambah besar tanpa batas.
Diberikan sebuah fungsi f(x) = 1/x2. Berikut pengamatan nilai fungsi f(x) untuk nilai – nilai x berikut.
x = 1 → f(x) = 1
x = 10 → f(x) = 0,01
x = 100 → f(x) = 0,0001
x = 1000 → f(x) = 0,000001
…
Dari fungsi f(x) diatas dapat dilihat bahwa nilai f(x) semakin mendekati 0, ketika x semakin besar. Sekarang coba perhatikan grafik fungsinya.
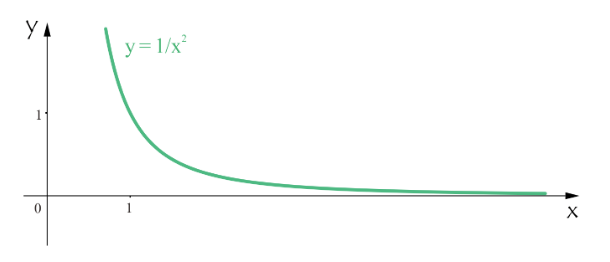
Sudah terlihat bahwa pada kurva y = 1/x2 semakin dekat dengan garis y = 0 dan x akan semakin besar.
Pada kenyataannya, seberapa besar x yang kita ambil, nilai 1/x2 akan semakin dekat ke 0.
Secara intuitif dapat di simpulkan, apbila x semakin besar tanpa batas, nilai 1/x2 semakin dekat ke 0. Pada notasi limit, pernyataan ini dapat ditulis seperti :
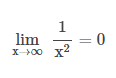
Sekarang mari kita amati nilai – nilai fungsi f(x) = 1/x2 untuk nilai-nilai x berikut.
x = -1 → f(x) = 1
x = -10 → f(x) = 0,01
x = -100 → f(x) = 0,0001
x = -1000 → f(x) = 0,000001
Dari data diatas dapat kita lihat bahwa f(x) = 1/x2 juga semakin dekat ke 0, ketika x semakin kecil (negatif besar). Dapat kita tulis
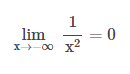
Nilai yang terdapat pada fungsi f(x) tidaklah selalu kearah mendekati bilangan yang tertentu saja, disaat x tersebut menjadi semakin membesar.
Bisa saja nilai pada f(x) akan menjadi semakin besar hingga terus – menerus bertambah besar tanpa batas. Untuk kasus seperti ini, dapat kita tulis
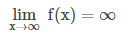
artinya jika nilai x itu dapat semakin besar hingga tanpa batas, maka akhirnya nilai pada f(x) juga akan semakin menjadi besar hingga ketanpa batas. Limit seperti ini disebut limit tak terhingga di tak hingga.
Fungsi Limit Tak Hingga
Seperti telah diuraikan di muka bahwa nilai limit berhingga suatu fungsi f(x) untuk x mendekati a didapat dengan cara mensubstitusikan nilai a ke fungsi f(x). Atau ditulis
Ini juga berlaku untuk limit tak hiingga suatu fungsi aljabar f(x) dan sehingga
Seperti contoh dibawah ini :
Apabila f(x) memiliki bentuk fungsi pecahan, maka nilai substitusinya akan memungkinkan hasil tak terdefinisi, yaitu bentuk
atau seperti :
Pada f(x) dimanipulasi dengan cara :
Apabila n ialah derajat tertinggi diantara g(x) atau h(x) maka g(x) dan h(x) masing – masing akan dibagi dengan xn .
Rumus Limit Tak Hingga
Limit Tak Hingga Bentuk Polinomial
Bentuk polinomial dalam variabel x pangkat tertinggi satu apabila digambarkan dalam diagram kartesius maka akan berbentuk garis lurus.
Nilai limit dalam bentuk polinomial tergantung berdasarkan dari pangkat yang tertinggi dari polinomial tersebut.
Limit fungsi yang memiliki variabel x nya akan berpengaruh secara langsung dalam fungsi f (x) nya.

Saat nila – nilai x menuju nilai yang sangat besar atau tak hingga, maka nilai 3 x juga akan menuju tak hingga.
Sedangkan x yang menuju negatif tak hingga maka nilai fungsi limit nya juga akan menuju nilai yang amat kecil yaitu negatif tak hingga.
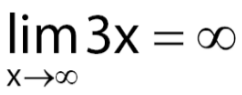

Limit Tak Hingga Bentuk Pecahan
Caranya untuk segera mendapatkan nilainya dalam bentuk pecahan dapat diperoleh dengan cara menyederhanakan suatu bentuk pecahan itu sendiri. Baca Juga : Fungsi Komposisi
Berikut ini ada cara yang lebih singkat agar menghasilkan nilai limit tak hiingga didalam bentuk sebuah pecahan.
Sebelumnya anda perlu memperhatikan dulu bagaimana cara mendapatkan nilainya dalam bentuk pecahan di bawah ini

Berikut merupakan tiga rumus cepat yang bisa anda gunakan. Pemakaiannya didasarkan dalam pangkat tertinggi variabel antara pembilang dan juga penyebut.
Secara singkat bisa dibuat rumus seperti berikut ini :
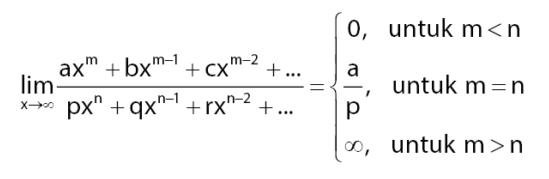
Limit Tak Hingga Trigonometri
Seperti halnya limit menuju ke suatu titik bentuk trigonometri, limit tak hiingga trigonometri juga memiliki kesamaan dasar yang dapat digunakan.
Agar bisa mengerjakan soal – soalnya dalam bentuk trigonometri, kesamaan ini dapat dilihat pada gambar di bawah ini
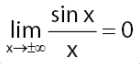
Dengan memakai persamaan yang ada di atas, anda bisa menentukan nilainya dalam berbagai macam tipe soal limit dengan bentuk trigonometri.
Limit Tak Hingga Pada Bentuk Eksponensial
Terdapat dua jenis bentuk pada soalnya didalam bentuk eksponensialnya yang akan kita bahas seperti dibawah ini.
Ide dalam mendapatkan nilaimya dalam bentuk eksponensial sama juga soalnya pada bentuk yang lainnya.
Apabila satu dibagi bilangan yang sangat besar maka akan dapat menghasilkan nilai – nilai limit 0.
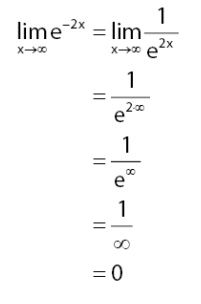
Bilangan yang sudah dipangkatkan dalam bilangan yang sangat besar maka akan menghasilkan bilangan yang sangat besar atau pun tak hingga.

Seperti itulah cara untuk menyelesaikan soal mengenai limit tak hiingga dengan berbagai macam cara yang dapat digunakan dalam mengerjakan soalnya. Baca Juga : Suku Banyak
Baik yang dapat digunakan pada bentuk polinomial, pecahan, trigonometri dan juga eksponensial.
Contoh Soal Limit Tak Hingga
- Tentukan hasil dari :

Pembahasan


2. Tentukan hasil dari :

Pembahasan


Pada contoh di atas, bisa disimpulkan bahwa pembahasan limit tak terhingga fungsi aljabar pecahan dapat ditentukan oleh koefisien dari variable pangkat tertinggi.
Supaya lebih jelasnya dapat dilihat pada contoh soal berikut dibawah ini :
3. Tentukan hasil dari :

Pembahasan
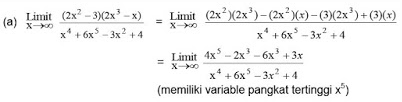
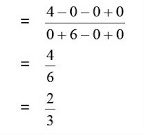

4. Tentukan hasil dari :

Pembahasan


Dari soal diatas dapat disimpulkan bahwa :
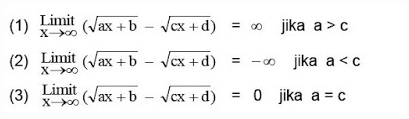
5Tentukan hasil dari :
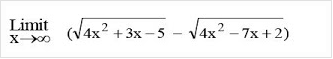
Pembahasan

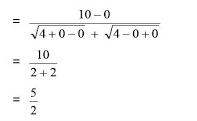
Dari soal diatas dapat disimpulkan bahwa :
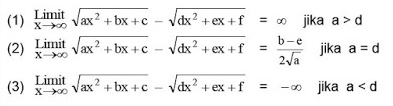
6. Tentukan hasil dari :
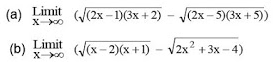
Pembahasan

Tak hingga bentuk polinomial dengan variabel x
Mungkin ini saja yang bisa edmodo sampaikan tentang materi matematika yang berjudul limit tak hingga. Semoga ulasan yang telah kami jelaskan ini dapat bermanfaat bagi sahabat semua.
Baca Juga :
