Identitas Trigonometri – Ialah merupakan salah satu dari cabang ilmu pelajaran matematika yaitu yang mempelajari tentang suatu hubungan diantara sisi dengan sudutnya dari sebuah bangun datar segitiganya serta berdasarkan fungsi dasarnya yang datang dari relasi itu sendiri.

Trigonometri ini juga sangat identik dengan fungsi trigonometri yang meliputi cosinus (cos), sinus (sin), tangen (tan), cotangen (cotan), secan (sec), serta cosecan (cosec).
Semua itu merupakan suatu cara untuk menentukannya pada suatu sisi, sebuah segitiga, dan sudut yang telah terbentuk dari dua sisi didalam sebuah segitiga.
Identitas Trigonometri
Dimana identitas ini sendiri merupakan sebuah landasan dasar dari hubungan balik.

Identitas trigonometri ialah merupakan sebuah relasi atau sebuah kalimat yang terbuka dan dapat memuat dari fungsi – fungsi trigonometri dan bernilai benar untuk setiap penggantian variabel dengan konstan anggota domain fungsinya.
Jadi kita perlu mengetahuinya bahwa pada kebenaran suatu relasi atau kalimat terbuka itu merupakan suatu identitas yang perlu dibuktikan kebenarannya.
Sejarah Trigonometri
Nama trigonometri ini diambil dari bahasa yunani yang terdiri atas kata trigonon dan juga metro, namun trigonono itu sendiri juga mempunyai arti yaitu tiga buah sudut dan sedangkan metro yang artinya ialah mengukur.
Namun ilmu ini juga merupakan salah satu dari cabang materi matematika yang bisa saling berhadapan dengan sebuah sudut segitiga dan fungsi dari trigonometriknya, adanya sudut ini dapat mencakup (sinus, cosinus dan tangen).
Dan trigonemetri ini juga mempunyai suatu hubungan dengan ilmu geometri, sebenernya ada ketidak setujuan tentang apa hubungannya pada sebagian besar orang sering menyebutkannya bahwa trigonometri itu sebernarnya menjadi salah satu dari bagian ilmu geometri.
Pada sejarahnya ini sangat sulit untuk di telusuri siapakah yang menemukan ilmuan ini pada pertama kali, dan yang pastinya ilmu trigonometri ini sudah ada pada zaman dahulu atau lebih tepatnya pada zaman mesir dan juga babilonia pada tiga ribu tahun yang lalu.
Namun pada seorang ilmuwan yunani dimasa Helenistik, yaitu Hipparchus pada tahun (190 SM – 120 SM) dan telah diyakini bahwa dari sebagian orang yang pertama kali menemukan teori tentang ilmu trigonometri ini karena keingin tahuannya pada dunia.
Sedangkan pada rumus (sinus, cosinus dan juga tangen) ini telah ditemukan oleh Surya Siddhanta yang merupakan seorang ilmuwan di india yang telah dipercaya dan hidup pada abad ke tiga sebelum masehi, dan yang selebihnya pada teori tentang trigonometri ini telah di sempurnakan oleh para ilmuwan – ilmuwan yang lainnya pada zaman berikutnya.
Perbandingan Trigonometri
Pada lingkaran dengan pusat O (0, 0) dan pada jari – jarinya (r), sedangkan pada titik A (x, y) serta pada lingkaran dan juga sudut dibentuk oleh OA terhadap sumbu X.
Pada berlaku r2 = x2 + y2 sehingga dapat diperoleh dengan perbandingan trigonometri, sebagai berikut ini :

Rumus Identitas Trigonometri
Dan pada rumus identitas trigonometri ini merupakan suatu rumus yang di gunakan untuk bisa menyatakan pada suatu fungsi antara satu fungsi dengan fungsi yang lainnya.
Contohnya seperti fungsi secan, yang mana pada fungsi ini bisa menjadi kebalikan dari apa fungsinya cosinus, ternyata hal ini juga bisa di berlakukan kepada fungsi kebalikannya pada yang lainnya.
Tidak hanya dari fungsi kebalikannya saja namun ada juga dari fungsi identitas trigonometri yang telah digunakan untuk menyatakan mengenai hubungan pada fungsi trigonometri, untuk berbagai hubungan pada persamaan tersebut bisa anda lihat dari rumus berikut ini yaitu.

Dari rumus diatas tadi merupakan suatu rumus turunannya yang didapatkannya dengan cara saling menghubungkan suatu fungsi dari trigonometri yang bersamaan dengan fungsi trigonometri pada lainnya, karena rumus ini merupakan fungsi identitas maka fungsi ini harus di buktikan kebenarannya.
Adapun cara untuk membuktikannya bisa dilakukan dengan cara merubah ruas kirinya suapaya menjadi sama dengan ruas kanannya.
Selain dari itu, dapat juga di lakukan dengan sebaliknya, sebenarnya masih banyak sekali fungsi dari identitas trigonometri.
Dibawah ini ialah merupakan rumus dari identitas trigonometri yang lainnya yang perlu anda ketahui.

Macam – Macam Rumus Identitas Trigonometri
Trigonometri ini juga mempunyai beberapa macam rumus, yaitu sebagai berikut ini :
Rumus Jumlah Dan Selisih Dua Sudut
- Rumus Untuk Cosinus Jumlah Dan Selisih Dua Sudut Yaitu :

- Rumus Untuk Sinus Jumlah Dan Selisih Dua Sudut Yaitu :

- Rumus Untuk Tangen Jumlah Dan Selisih Dua Sudut Yaitu :
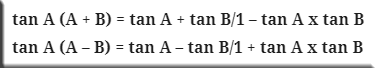
Rumus Trigonometri Untuk Sudut Rangkap
- Dengan Mempergunakan Rumus sin (A + B) Untuk A = B :
Sin 2A = Sin (A + B)
= Sin A Cos A + Cos A Sin A
= 2 Sin A Cos A
Jadi, Sin 2A = 2 Sin A Cos A
- Dengan Mempergunakan Rumus cos (A + B) Untuk A = B :
Cos2A=Cos(A+A)
= Cos A Cos A – Sin A Sin
= Cos 2A – Sin 2A …… (1)
Atau
Cos2A=Cos 2A – Sin 2A
= Cos 2A – (1 – Cos 2A)
= Cos 2A – 1 + Cos 2A
= 2 Cos 2A – 1 …… (2)
Atau
Cos2A=Cos 2A – Sin 2A
= (1 – Sin 2A) – Sin 2A
= 1 – 2 Sin 2A …… (3)
Dari Peramaan (1), (2), dan (3) diatas di dapatkan rumus yaitu :
Cos2A=Cos 2A – Sin 2A
= 2 Cos 2A – 1
= 1 – 2 Sin 2A
- Dengan Mempergunakan Rumus Tan (A + B) Untuk A = B Yaitu :
Tan 2A = Tan (A + A)
= Tan A + Tan A/1 Tan A x Tan A
= 2 Tan A/1 – Tan 2A
Jadi, Tan 2A = 2 Tan A/1 – Tan 2A
Contoh Soal Identitas Trigonometri
Apabila Tan 5° = p. Maka tentukanlah :
- Tan 50°
Penyelesaiannya :
Tan 50° = Tan (45° + 5°)
= Tan 45° + Tan 5°/1 – Tan 45° x Tan 5°
= 1 + p/1 – p
Jadi, hasilnya ialah = 1 + p/1 – p
Sekian yang bisa edmodo.id sampaikan pada pembahasan kali ini mengenai Identitas Trigonometri, semoga dapat bermanfaat untuk semuanya.
Baca Juga :
