Cosinus

Cosinus – Apakah kamu tahu apa yang dimaksud dengan cosinus ?

Cosinus didalam pelajaran matematika ialah suatu perbandingan pada sisi segitiga yang letaknya terdapat disudut yang mempunyai sisi miring.

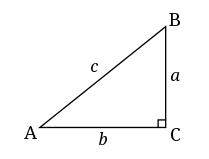
Perhatikanlah segitiga pada gambar diatas. Menurut definisinya, cosinus pada gambar diatas diketahui nilai cosinusnya merupakan nilai cosinus yang positif dikuadran I beserta IV dan yang negatif berada dikuadran II juga III.

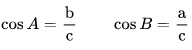
Hubungan cosinus terhadap sekan :

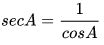
Aturan Cosinus

Menurut hukum cosinus, atau biasa disebut dengan aturan kosinus didalam trigonometri merupakan aturan yang harus memberikan suatu keterkaitan hubungan yang berlaku didalam sebuah segitiga, yakni misalnya diantara panjang sisi – sisi segitiganya dan terdapat cosinus di salah satu sudut yang ada didalam segitiganya itu.

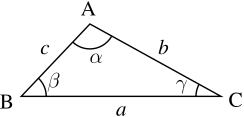
Perhatikanlah gambar segitiga yang ada diatas.

Menurut aturan cosinusnya menyatakan bahwa :

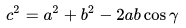
Dengan y merupakan sebuah sudut yang dibentuk dari sisi a, sisi b, dan juga sisi c ialah sisi – sisi yang saling berhadapan dengan sudut y tersebut. Baca Juga : SPLDV

Aturannya juga berlaku sama pada sisi a dan b :

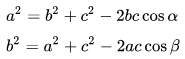
Dan bisa dikatakan cosinus juga, apabila panjang pada dua sisinya itu memiliki sebuah sudut segitiga yang diapit dengan kedua sisinya tu diketahui.

Seharusnya dapat dengan mudah menentukan suatu panjang sisi yang lainnya.

Namun kebalikannya, apabila panjang ditiga sisi tersebut diketahui, maka dengan mudah dapat menentukan nilai besaran sudut didalam segitiganya itu.

Caranya dengan mengubah aturan cosinusnya yang tadi sedikit saja, misalnya :

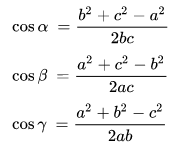
Aturan Cosinus Pertama

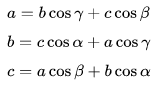
Aturan Cosinus Kedua

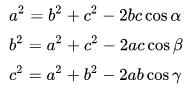
Tabel Cosinus

Maka dari itu berikut ini tabel cos sin tan dengan seluruh sudut yang terbentuk didalam satu lingkaran penuh atau sering dinamakan dengan lingkaran 360º. 

Tabel Sin Cos Tan Kuadran 1 dari 0º sampai 90º

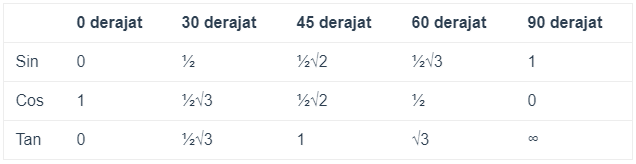
Tabel Sin Cos Tan Kuadran 2 dari 90º sampai 180º

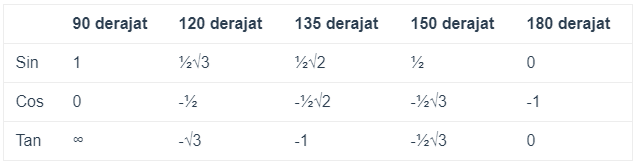
Tabel Sin Cos Tan Kuadran 3 dari 180º sampai 270º

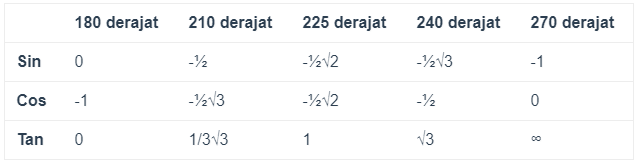
Tabel Sin Cos Tan Kuadran 4 dari 270º sampai 360º

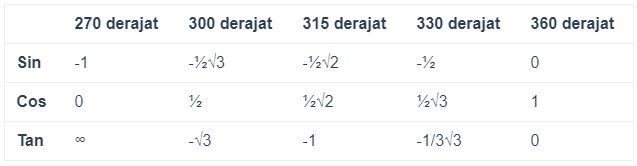
Tabel – tabel diatas yang mencangkup sin cos tan trigonometri pada pelajaran matematika di tingkat SMA dapat berguna serta memudahkan didalam menghitung suatu perhitungan sudut bangun dengan sudut istimewa trigonometri.

Tabel Sin Cos Tan Sudut Istimewa

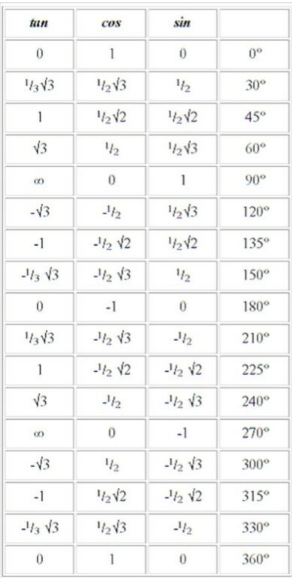
Apabila penjelasan pada tabel yang diatas itu diuraikan secara 4 kuadran, dan apabila digabungkan inilah hasil dari penggabungan tabel tersebut, lihatlah tabel sudut istimewa dibawah ini.

Rumus Cosinus

Pada gambar segitiga siku – siku atau segitiga yang memiliki sudut 90º diatas itu, jadi nilai dari cosinus yang memilikai nilai perhitungan seperti iitu ialah cosA=b/c dan cosB=a/c.

Melainkan untuk mendapatkan cara mencari nilai dari cosinus positif dapat saja ditemukan pada kuadran I dan juga IV, sebab kuadran I dan IV itu merupakan sebuah Tabel Sudut Istimewa pada Trigonometri.

Sedangkan cara menghitung sebuah nilai cosinus negatif itu dapat dilihat pada kuadran II serta kuadran III, sebab kuadran II dengan kuadran III itu merupakan sebuah Tabel Sudut Istimewa pada Trigonometri.

Rumus Menghitung Nilai Cosinus Trigonometri

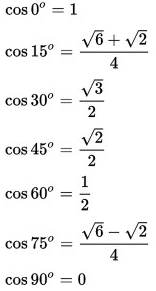
Dari gambar diatas itu menjelaskan tentang rumus cosinus trigonometri pada pelajaran matematika, sedangkan untuk nilai cos 0º, nilai cos 15º, nilai cos 30º, nilai 45º, nilai 60º, nilai 75º beserta nilai 90º ialah nilai – nilai cosinus menurut sudut istimewa trigonometri. Baca Juga : Pertidaksamaan

Contoh Soal Cosinus

Berikut ini beberapa contoh soal tentang pembahasan cosinus, yang diantaranya :

Contoh Soal 1

Apabila pada segitiga ABC, berlaku a2 = b2 + c2 − √3bc dan c2 = a2 + b2 − ab, maka bisakah kamu tentukan besar sudut B itu? …

Jawabannya :

Menurut aturan pada cosinus, panjang sisi a dapat dihitung dengan menggunakan rumus a2 = b2 + c2 − 2bc cos A, sebab pada soal ini diketahui a2 = b2 + c2 − √3bc, jadi dapat berlaku :

• 2bc cos A = √3bc
• cos A = (√3bc) / 2bc
• cos A = ½√3
• A = 30º

Menurut aturan pada cosinus, panjang sisi c dapatlah dihitung dengan menggunakan rumus c2 = a2 + b2 − 2ab cos C, sebab pada soal ini diketahui c2 = a2 + b2 − ab, jadi dapat berlaku :

2ab cos C = ab
cos C = (ab) / 2ab
cos C = ½
C = 60º

Sedangkan menurut jumlah sudut segitiganya :

A + B + C = 180º
B = 180º

• (A + C)
  B = 180º
• (30º + 60º)
  B = 180º
• 90º
  B = 90º
  Jawabannya, besar sudut B ialah 90º.

Contoh Soal 2

Apabila panjang a, b, dan juga c didalam segitiga ABC itu berturut – turut ialah 8cm, 7cm, lalu 4cm, lalu berapakah besar sudut A itu? …

Jawabannya :

Diketahui :

• a=8cm
• b=7cm
• c=4cm

Menurut aturan cosinusnya :

• cos A = (b2 + c2 − a2) / 2bc
• cos A = (72 + 42 − 82) / 2(7)(4)
• cos A = (49 + 16 − 64) / 56
• cos A = 1/56
• cos A = 0,017
• A = 89º

Hasilnya, besar sudut A ialah 89º

Contoh Soal 3

Apabila panjang sisi a didalam segitiga ABC ialah setengah dari panjang sisi b dan besaran sudut c ialah 60º, tentukan hubungan diantara panjang sisi a dan c yang benar itu ialah? ….

Jawabannya :

Diketahui :

• b=2a
• c=60º

Menurut aturan cosinusnya :

• c2 = a2 + b2 − 2ab cos C
• c2 = a2 + (2a)2 − 2a(2a) cos 60º
• c2 = a2 + 4a2 − 4a2(0,5)
• c2 = 5a2 − 2a2
• c2 = 3a2
• c = √3 a

Hasilnya hubungan diantara panjang a dan c ialah √3 a.

Mungkin ini saja yang dapat edmodo sampaikan kali ini mengenai materi cosinus ini, semoga materi yang edmodo sampaikan kali ini dapat bermanfaat untuk sahabat sekalian belajar dirumah. Terima kasih.

Baca Juga : Dimensi Tiga